Acting in Delayed Environments with Non-Stationary Markov Policies

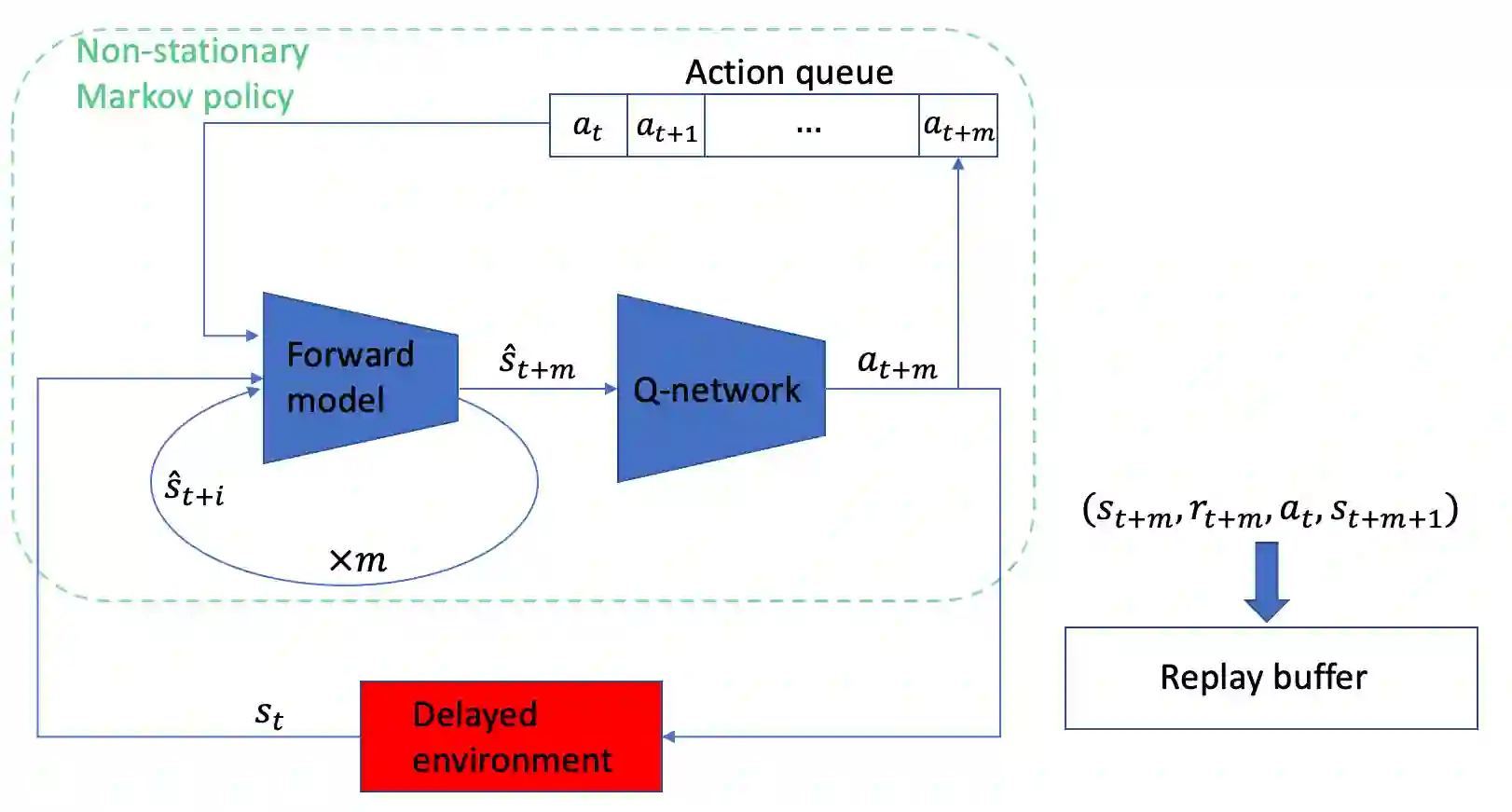
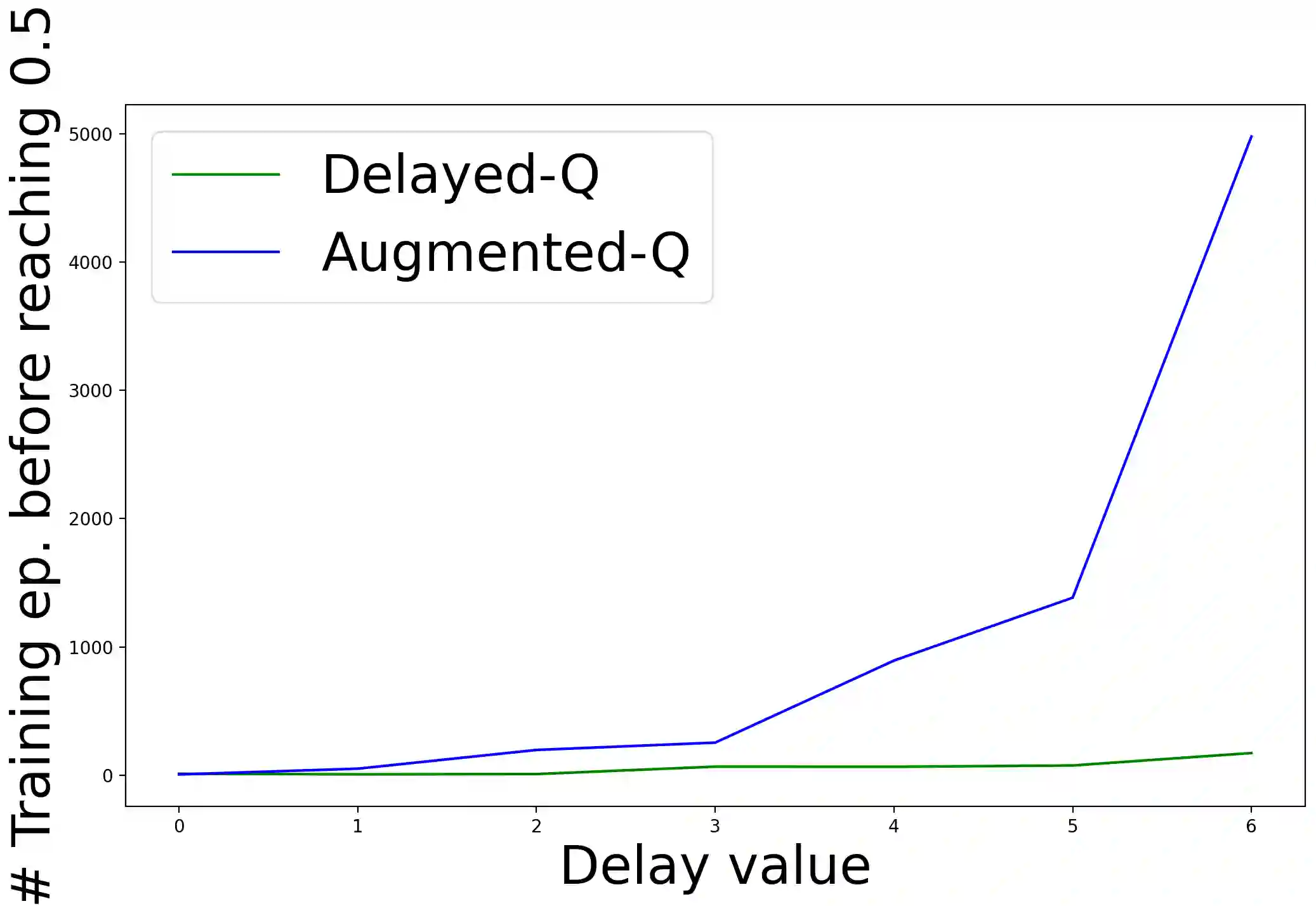
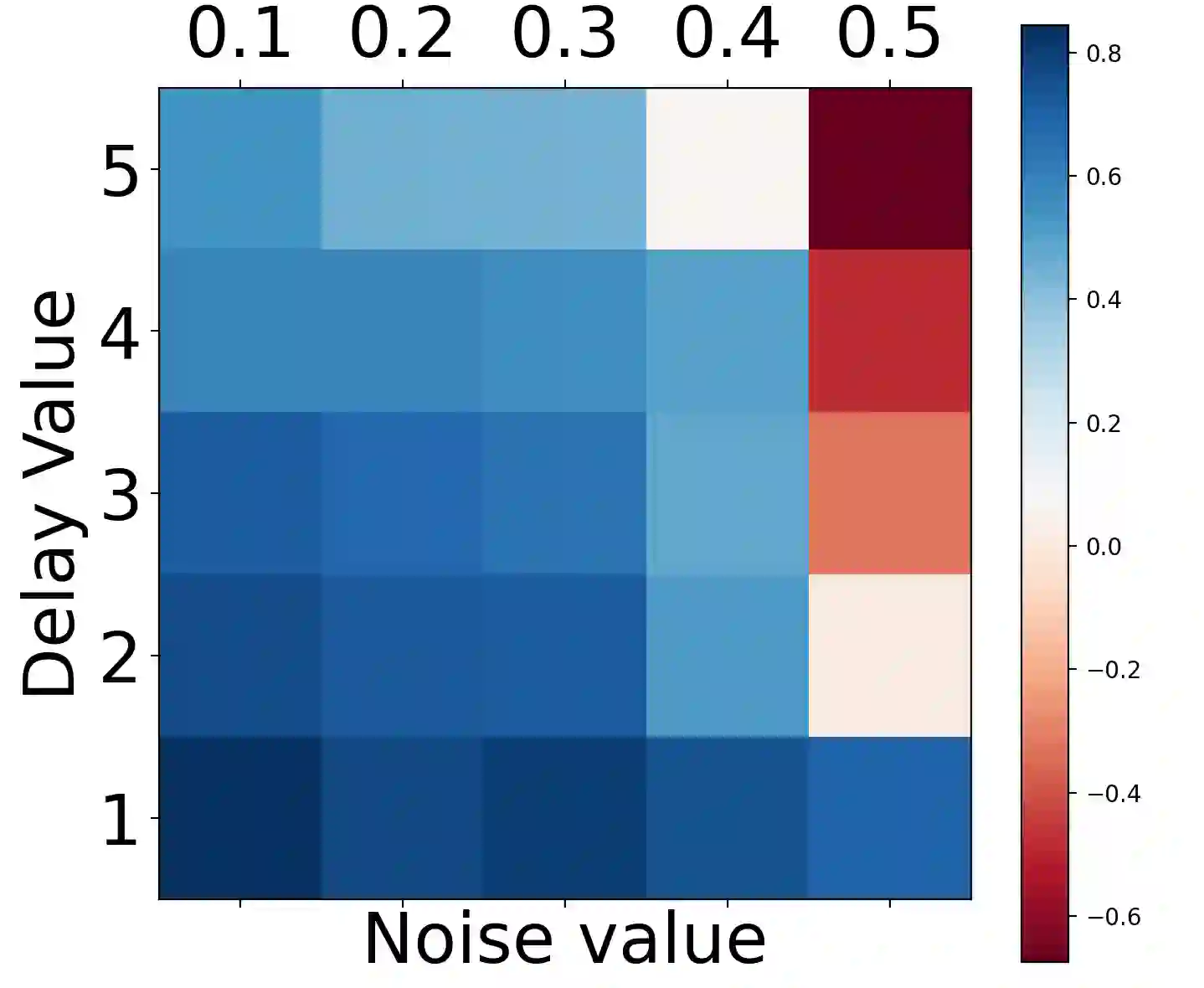
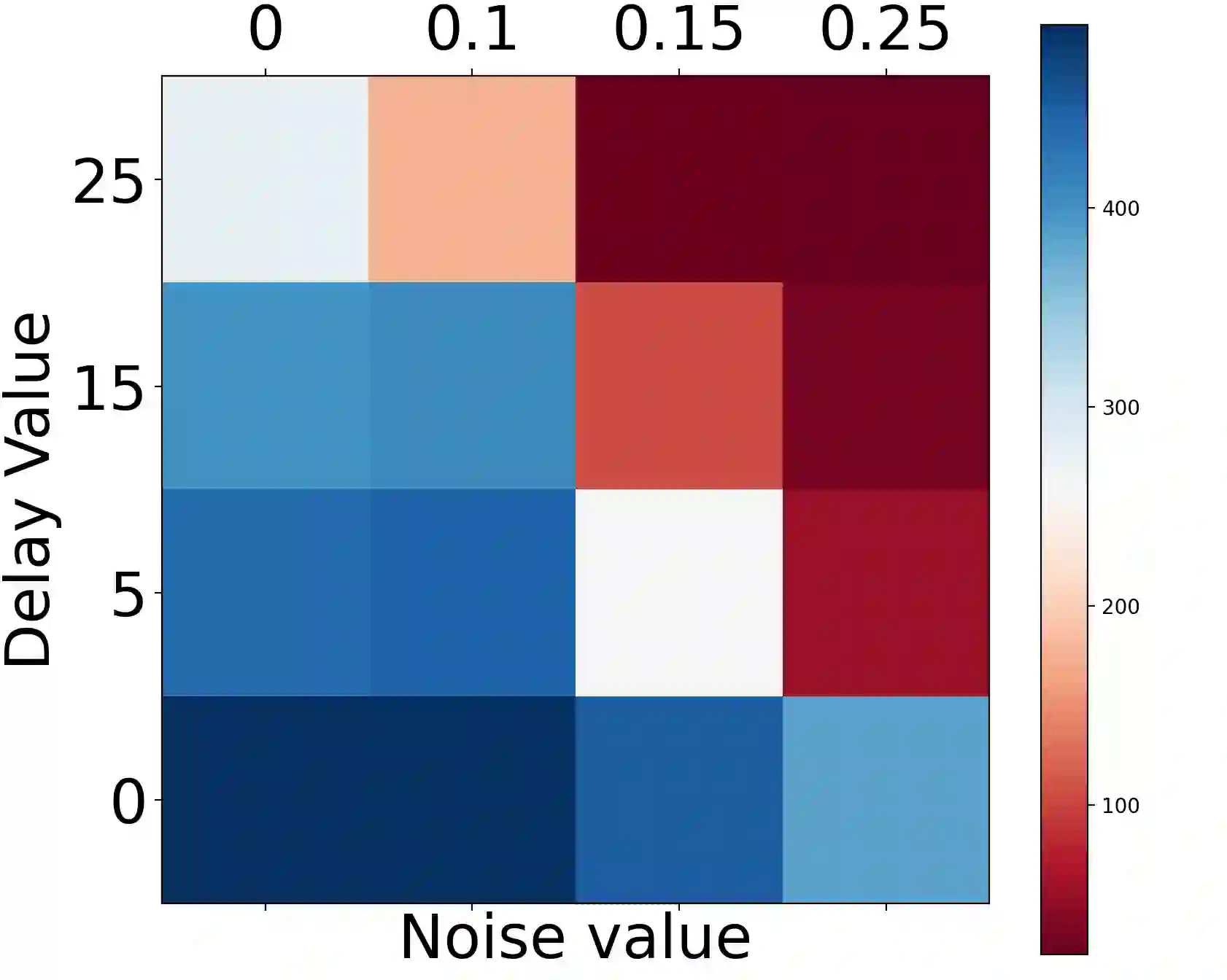
The standard Markov Decision Process (MDP) formulation hinges on the assumption that an action is executed immediately after it was chosen. However, assuming it is often unrealistic and can lead to catastrophic failures in applications such as robotic manipulation, cloud computing, and finance. We introduce a framework for learning and planning in MDPs where the decision-maker commits actions that are executed with a delay of $m$ steps. The brute-force state augmentation baseline where the state is concatenated to the last $m$ committed actions suffers from an exponential complexity in $m$, as we show for policy iteration. We then prove that with execution delay, Markov policies in the original state-space are sufficient for attaining maximal reward, but need to be non-stationary. As for stationary Markov policies, we show they are sub-optimal in general. Consequently, we devise a non-stationary Q-learning style model-based algorithm that solves delayed execution tasks without resorting to state-augmentation. Experiments on tabular, physical, and Atari domains reveal that it converges quickly to high performance even for substantial delays, while standard approaches that either ignore the delay or rely on state-augmentation struggle or fail due to divergence. The code is available at https://github.com/galdl/rl_delay_basic.git.