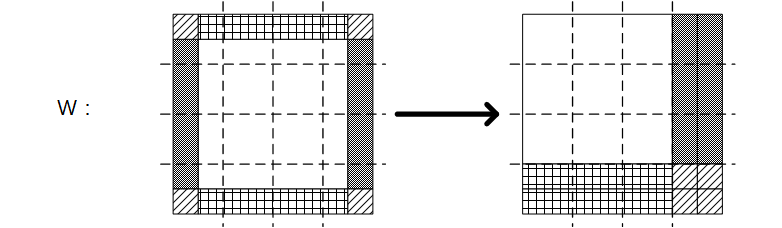
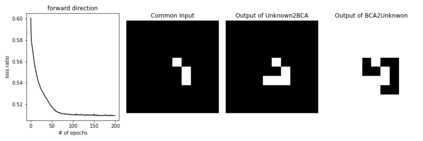In this paper, we will consider the machine learning system that can learn fundamental physics theory based on cellular automaton interpretation (CAI). First, assuming that we can calculate the time-evolved cellular automaton (CA) for any initial CA by knowing the time-evolution law of the given system, we will show that there exists a convolutional neural network (CNN) architecture that can learn the time-evolution law of this system with only the calculated data set for a certain example. Finding a CNN architecture that can learn CA is equivalent to showing that a time-varying time-evolution operator can be represented as a finite composition of time-independent linear functions and ReLU type non-linear functions. As a concrete example, block CA, which is time reversible and expressed as a matrix multiplication that changes with time, will be used as the time-evolution law, and the CNN architecture that can learn this evolution law will be proposed. However, by the universal approximation theorem, even with data of arbitrary quantum systems, if the depth of the network is deep enough, a CNN architecture that can learn actual rules can be found, regardless of the Hamiltonian, and therefore, the time-evolution law can be consistently expressed as a CNN. Also, since the convolution layer can be expressed in a covariant form, it could be helpful to find a CNN architecture that can learn the evolution law for a data set that includes gravity. Meanwhile, it will be shown that if the activation function of the first and last hidden layer is bypass, the CNN can be trained to include the corresponding part of the probabilistic interpretation in conventional quantum mechanics. Finally, for the CA model in which the dimensional reduction in quantum gravity is first presented, we will discuss the CNN architecture that can find the non-trivial evolution law in a deductive way.
翻译:在本文中,我们将考虑一个机器学习系统,这个系统可以学习基于蜂窝自动图解(CAI)的基本物理理论。首先,假设我们可以通过了解给定系统的时间演变法,来计算任何初始 CA 的时间变化变异的细胞进化自动自动自动自动自动自动自动自动自动自动自动系统。我们将显示,存在一个能够学习这个系统的时间进化法的大脑神经网络(CNN)架构,只有为某个特定示例的计算数据集才能学习这个系统的时间进化法。找到一个能够学习CA的CNN结构。找到一个能够学习CAA的CNN结构,相当于显示一个时间翻转的时序运行操作操作操作器,可以代表一个时间翻转的内向时间变化操作操作器的有限构成,一个时间变化运行自久远的直径线函数和 ReLU 类型非线性功能。作为一个具体的例子,CA区块,可以追溯到时间变变变法的系统,这个结构可以持续地演化自动自动自动自动自动自动自动自动自动自动以来的变压结构的,而演化自动自动自动自动自动的,也可以演。