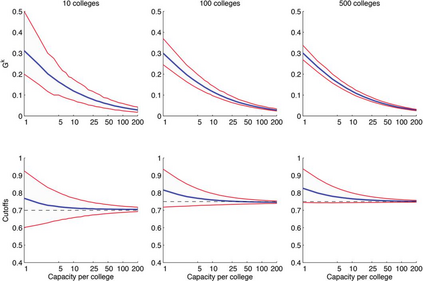
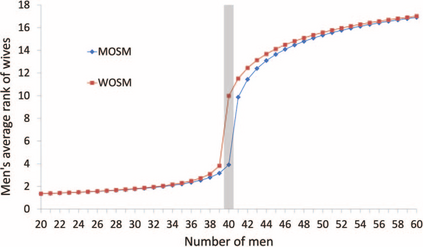
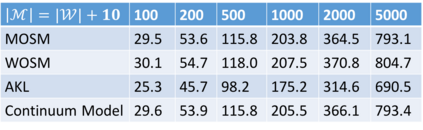
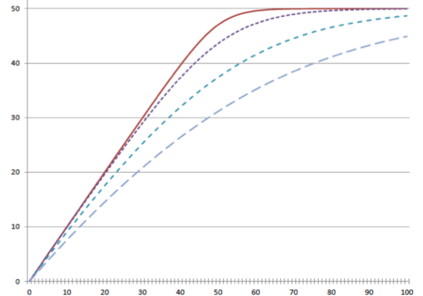
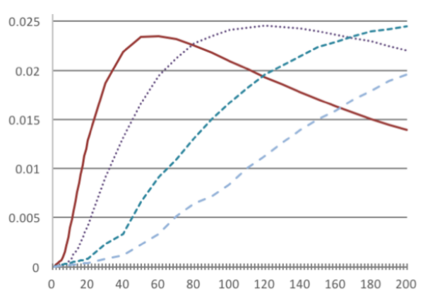
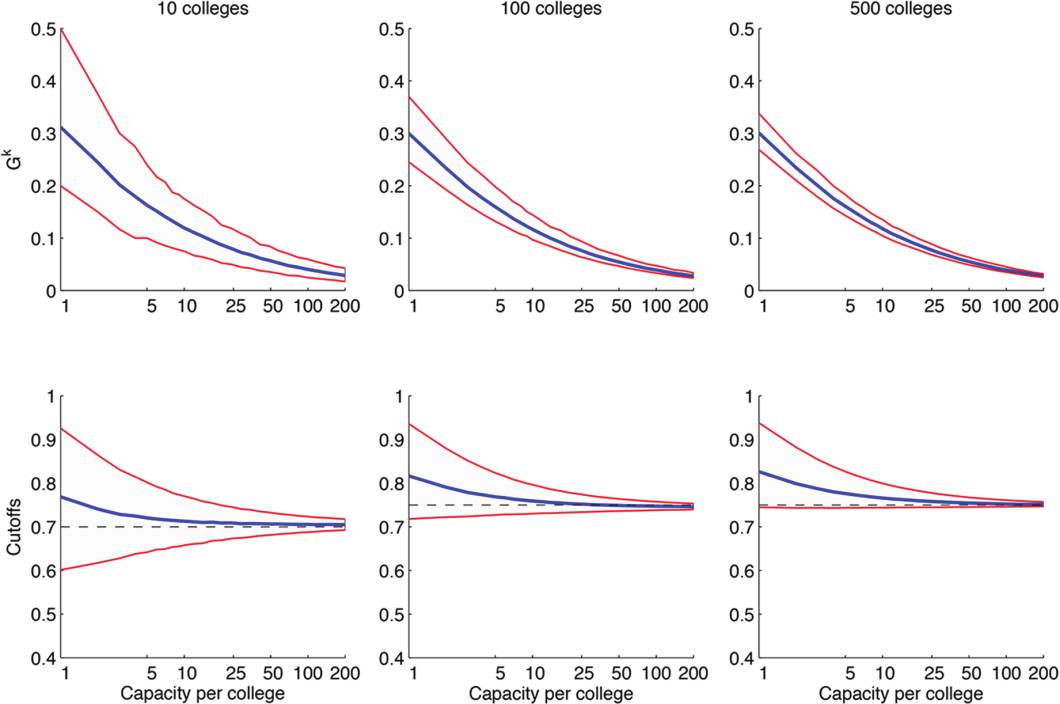
This paper introduces a unified framework for stable matching, which nests the traditional definition of stable matching in finite markets and the continuum definition of stable matching from Azevedo and Leshno (2016) as special cases. Within this framework, I identify a novel continuum model, which makes individual-level probabilistic predictions. This new model always has a unique stable outcome, which can be found using an analog of the Deferred Acceptance algorithm. The crucial difference between this model and that of Azevedo and Leshno (2016) is that they assume that the amount of student interest at each school is deterministic, whereas my proposed alternative assumes that it follows a Poisson distribution. As a result, this new model accurately predicts the simulated distribution of cutoffs, even for markets with only ten schools and twenty students. This model generates new insights about the number and quality of matches. When schools are homogeneous, it provides upper and lower bounds on students' average rank, which match results from Ashlagi, Kanoria and Leshno (2017) but apply to more general settings. This model also provides clean analytical expressions for the number of matches in a platform pricing setting considered by Marx and Schummer (2021).
翻译:本文引入了稳定匹配的统一框架, 将有限市场稳定匹配的传统定义和与Azevedo和Leshno(Leshno)稳定匹配的连续定义作为特例嵌入。 在此框架内, 我确定了一个新的连续模式, 进行个人水平概率预测。 这个新模式总是有独特的稳定结果, 使用延迟接受算法的模拟方法可以找到。 这个模式与 Azevedo 和 Leshno( Leshno) 之间的关键区别是, 他们假定每个学校的学生兴趣是确定性的, 而我提议的替代方法则假定它遵循Poisson的分布法。 因此, 这个新模式准确预测了模拟的截取分布, 即使只有10所学校和20名学生的市场也是如此。 这个模式对匹配的数量和质量产生了新的洞见。 当学校是同质时, 它提供了学生平均等级的上下限, 与Ashlagi、 Kanoria和Leshno( 2017年) 和Leshno( 2017年) 相匹配, 但适用于更普遍的环境。 这个模式也为Marx 和Schemmer( 2021) 的平台定价设置中的匹配点提供了干净的分析表达。 (2021) 。