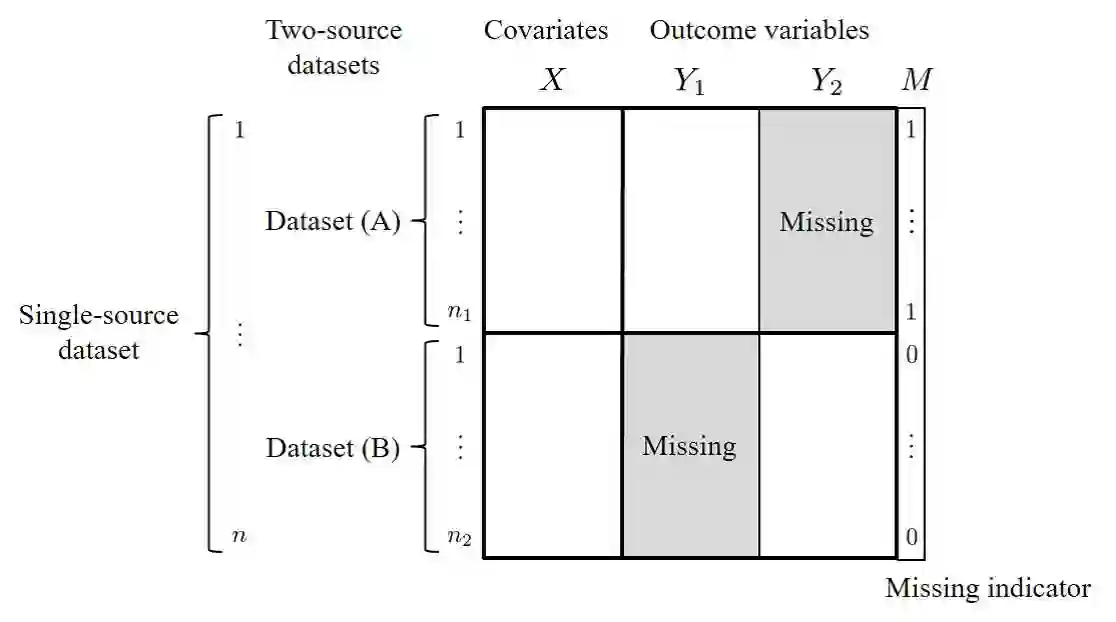
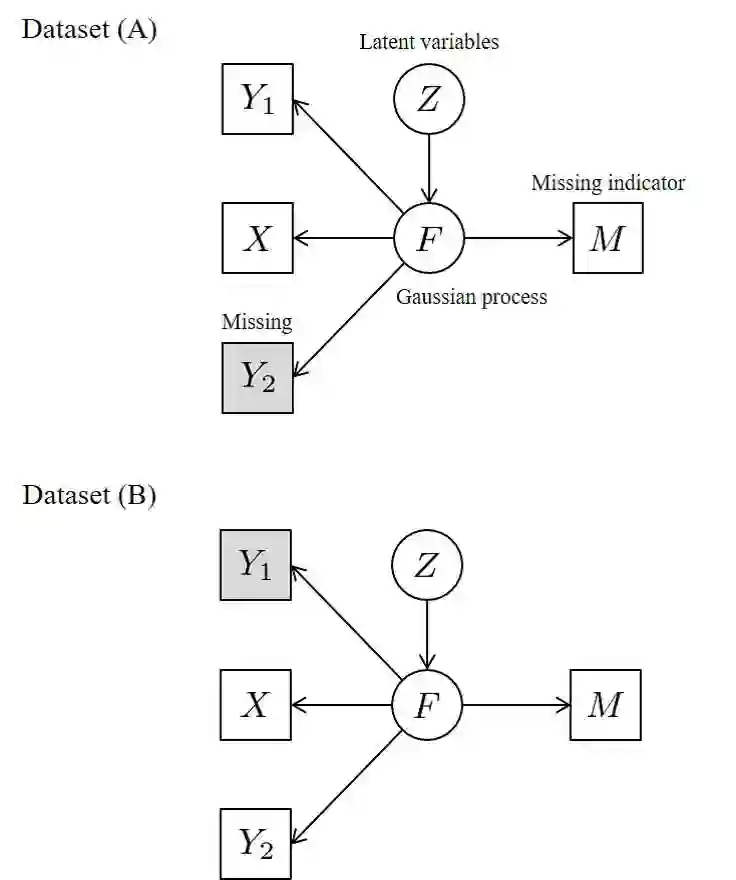
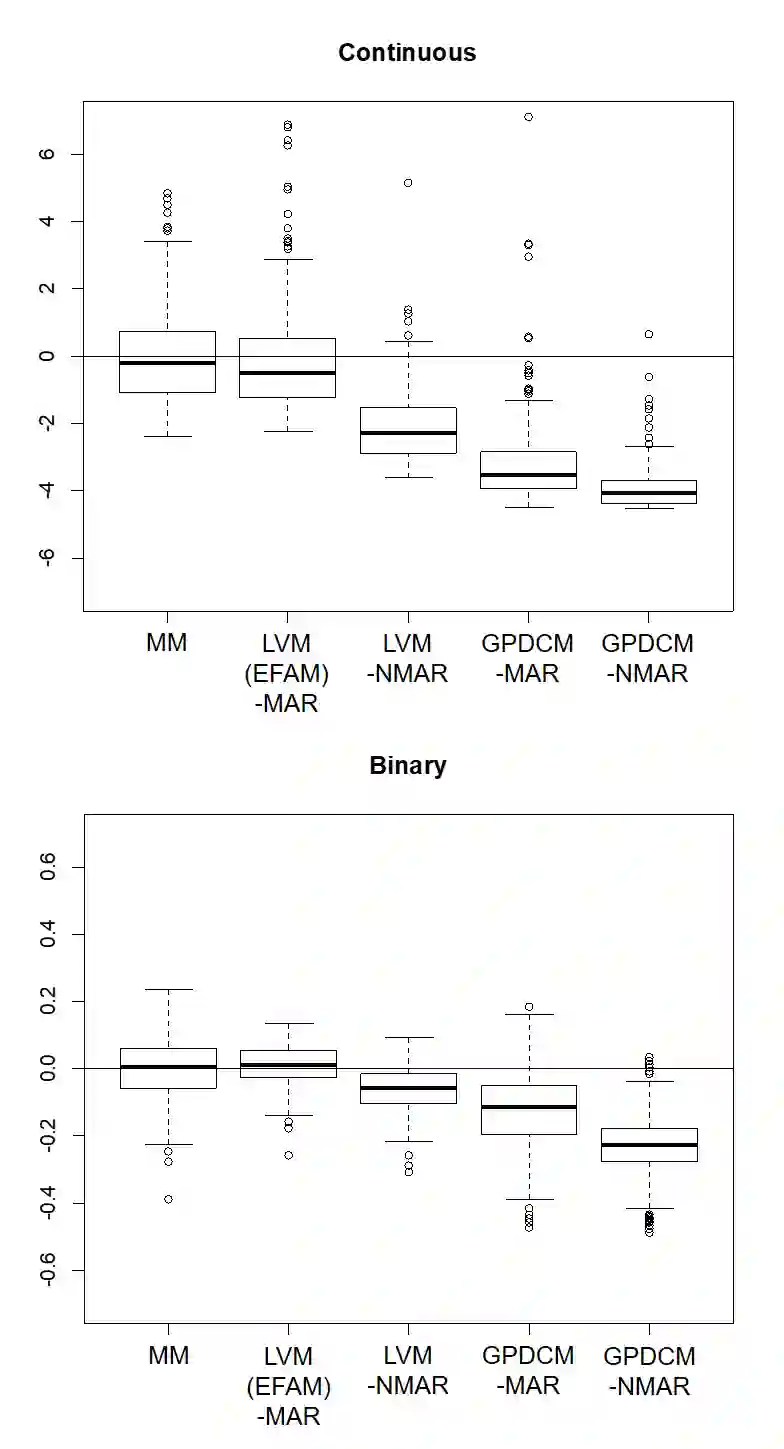
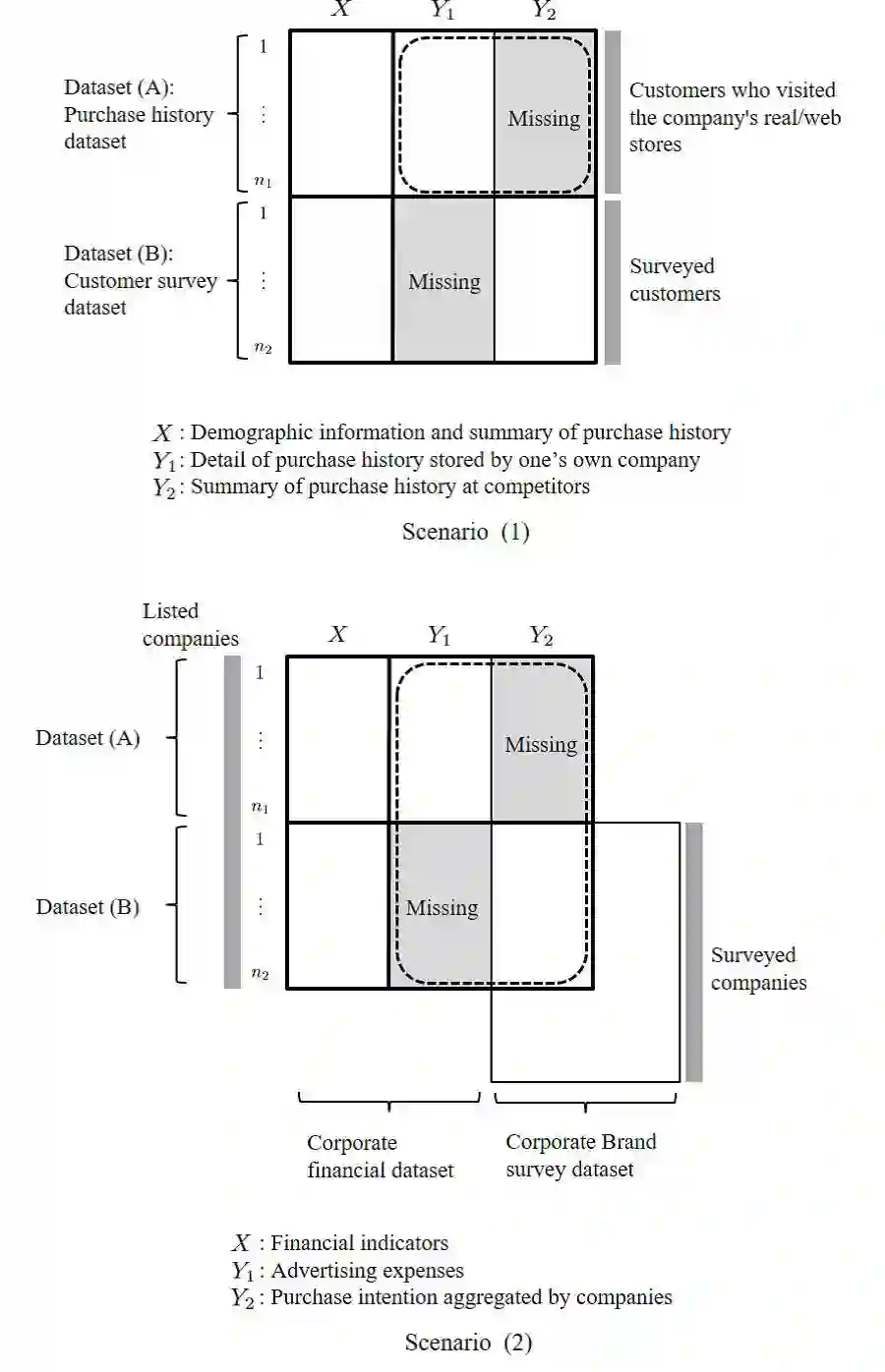
In the analysis of observational data in social sciences and businesses, it is difficult to obtain a "(quasi) single-source dataset" in which the variables of interest are simultaneously observed. Instead, multiple-source datasets are typically acquired for different individuals or units. Various methods have been proposed to investigate the relationship between the variables in each dataset, e.g., matching and latent variable modeling. It is necessary to utilize these datasets as a single-source dataset with missing variables. Existing methods assume that the datasets to be integrated are acquired from the same population or that the sampling depends on covariates. This assumption is referred to as missing at random (MAR) in terms of missingness. However, as will been shown in application studies, it is likely that this assumption does not hold in actual data analysis and the results obtained may be biased. We propose a data fusion method that does not assume that datasets are homogenous. We use a Gaussian process latent variable model for non-MAR missing data. This model assumes that the variables of concern and the probability of being missing depend on latent variables. A simulation study and real-world data analysis show that the proposed method with a missing-data mechanism and the latent Gaussian process yields valid estimates, whereas an existing method provides severely biased estimates. This is the first study in which non-random assignment to datasets is considered and resolved under resonable assumptions in data fusion problem.
翻译:在分析社会科学和企业的观测数据时,很难获得“(qisi)单一源数据集”,其中同时观察感兴趣的变量。相反,通常为不同的个人或单位获取多源数据集。提出了各种方法来调查每个数据集中变量之间的关系,例如,匹配和潜在的变量建模。有必要将这些数据集作为缺少变量的单一源数据集使用。现有方法假定,要整合的数据集是从同一人群中获取的,或抽样取决于变量。这一假设在随机(MAR)中被指为缺失的缺失。然而,正如应用研究所显示的那样,这一假设可能没有保存在实际数据分析中,而获得的结果可能存在偏差。我们提出的数据组合方法并不假定数据集是同质的。我们用高斯进程潜在变量模型来计算非MAR失踪的数据。这一模型假设,关注的变量和缺失概率取决于潜在变量,而在潜在变量中,这种假设在应用研究中,一个模拟式数据分析和现有数据分析方法提供了一种真实数据流率分析方法。一种模拟式数据分析,它提供了一种模拟式数据分析方法,而现有数据测算法则提供了一种稀有的模拟数据流分析方法。