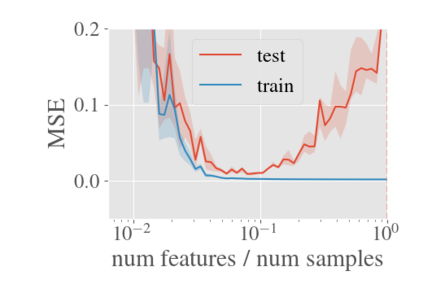
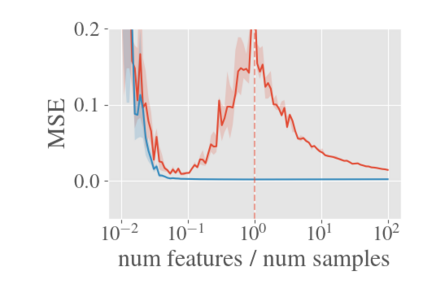
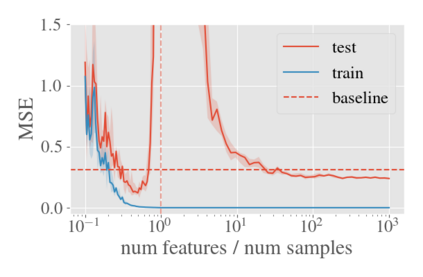
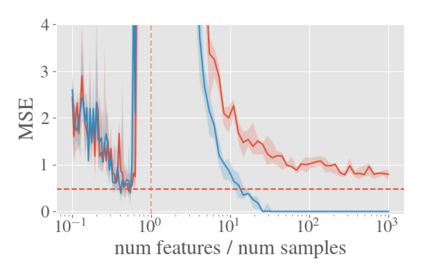
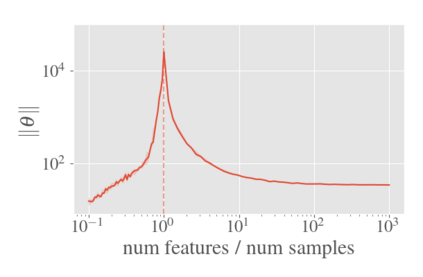
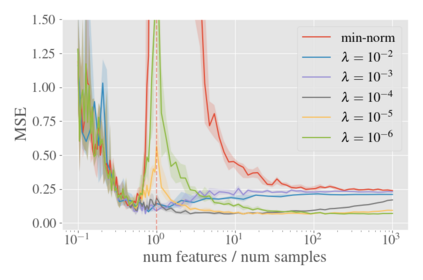
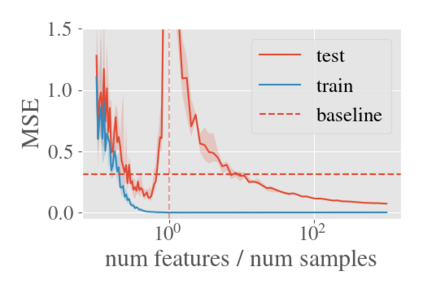
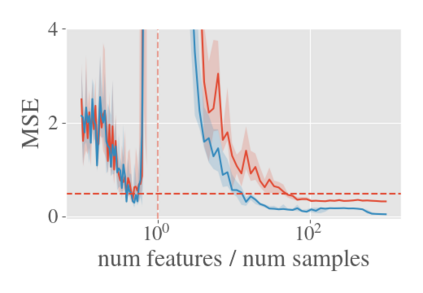
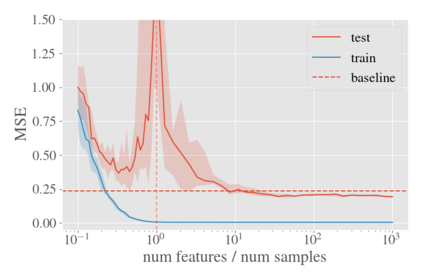
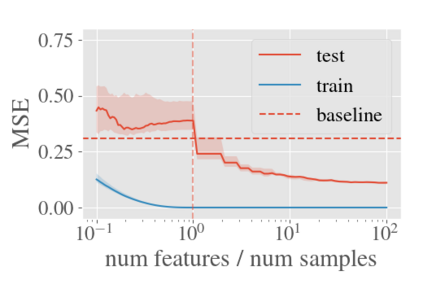
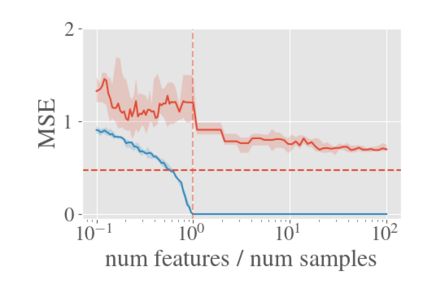
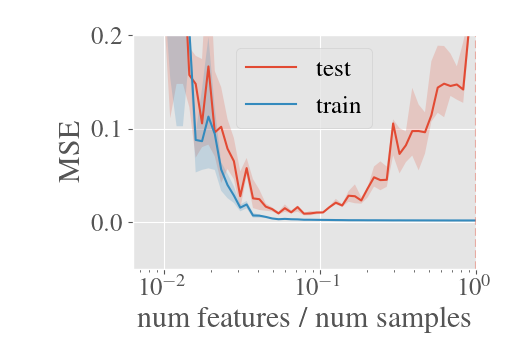
System identification aims to build models of dynamical systems from data. Traditionally, choosing the model requires the designer to balance between two goals of conflicting nature; the model must be rich enough to capture the system dynamics, but not so flexible that it learns spurious random effects from the dataset. It is typically observed that the model validation performance follows a U-shaped curve as the model complexity increases. Recent developments in machine learning and statistics, however, have observed situations where a "double-descent" curve subsumes this U-shaped model-performance curve. With a second decrease in performance occurring beyond the point where the model has reached the capacity of interpolating - i.e., (near) perfectly fitting - the training data. To the best of our knowledge, such phenomena have not been studied within the context of dynamic systems. The present paper aims to answer the question: "Can such a phenomenon also be observed when estimating parameters of dynamic systems?" We show that the answer is yes, verifying such behavior experimentally both for artificially generated and real-world datasets.
翻译:传统上,选择模型需要设计者平衡两个相互冲突的目标;模型必须足够丰富,足以捕捉系统动态,但不能灵活到能够从数据集中了解虚假随机效应。通常会发现模型验证性能在模型复杂性增加时遵循U形曲线。但机器学习和统计方面的最新发展观察到了“双白”曲线将U型模型性能曲线进行分包的情况。在模型达到内插能力(即,(近)完全适合培训数据)之后,性能又出现了第二次下降。据我们所知,这种现象并未在动态系统范围内研究。本文旨在回答以下问题:“在估计动态系统的参数时,是否也能观察到这种现象?”我们表明答案是肯定的,从实验角度对人工生成的和实际世界数据集进行这种行为进行验证。