Higher-Order Orthogonal Causal Learning for Treatment Effect

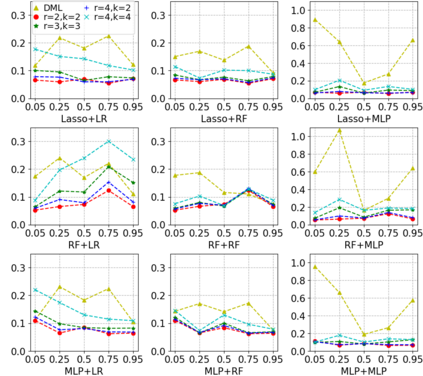
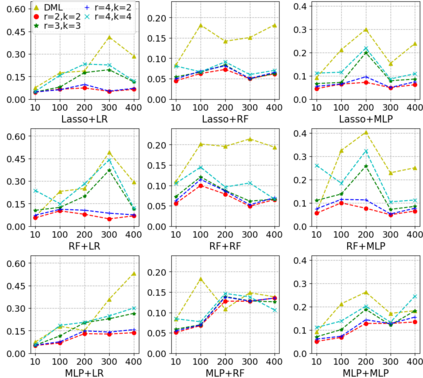
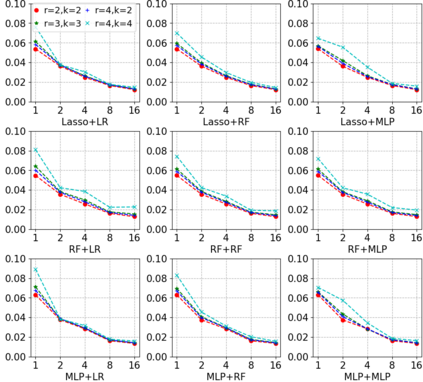
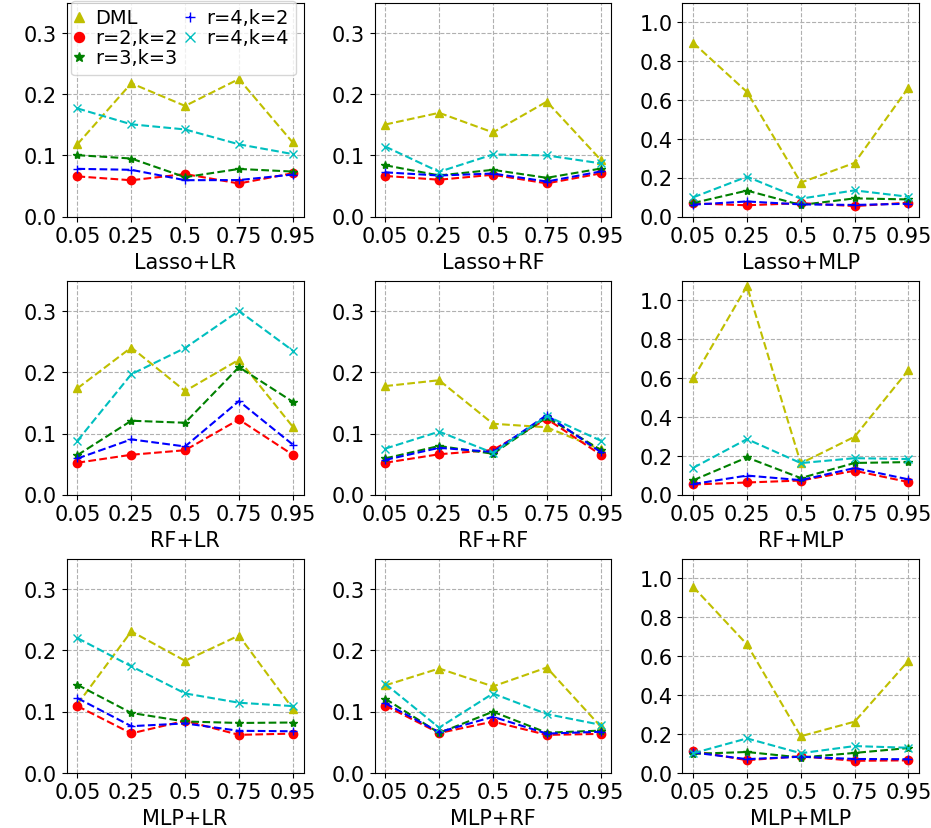
Most existing studies on the double/debiased machine learning method concentrate on the causal parameter estimation recovering from the first-order orthogonal score function. In this paper, we will construct the $k^{\mathrm{th}}$-order orthogonal score function for estimating the average treatment effect (ATE) and present an algorithm that enables us to obtain the debiased estimator recovered from the score function. Such a higher-order orthogonal estimator is more robust to the misspecification of the propensity score than the first-order one does. Besides, it has the merit of being applicable with many machine learning methodologies such as Lasso, Random Forests, Neural Nets, etc. We also undergo comprehensive experiments to test the power of the estimator we construct from the score function using both the simulated datasets and the real datasets.