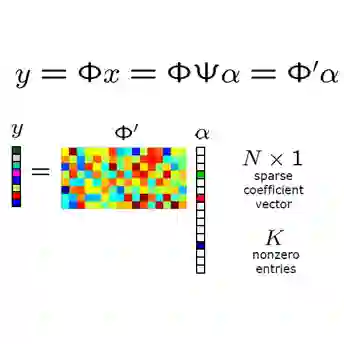
In this paper, we present a communication-efficient federated learning framework inspired by quantized compressed sensing. The presented framework consists of gradient compression for wireless devices and gradient reconstruction for a parameter server (PS). Our strategy for gradient compression is to sequentially perform block sparsification, dimensional reduction, and quantization. Thanks to gradient sparsification and quantization, our strategy can achieve a higher compression ratio than one-bit gradient compression. For accurate aggregation of the local gradients from the compressed signals at the PS, we put forth an approximate minimum mean square error (MMSE) approach for gradient reconstruction using the expectation-maximization generalized-approximate-message-passing (EM-GAMP) algorithm. Assuming Bernoulli Gaussian-mixture prior, this algorithm iteratively updates the posterior mean and variance of local gradients from the compressed signals. We also present a low-complexity approach for the gradient reconstruction. In this approach, we use the Bussgang theorem to aggregate local gradients from the compressed signals, then compute an approximate MMSE estimate of the aggregated gradient using the EM-GAMP algorithm. We also provide a convergence rate analysis of the presented framework. Using the MNIST dataset, we demonstrate that the presented framework achieves almost identical performance with the case that performs no compression, while significantly reducing communication overhead for federated learning.
翻译:在本文中,我们提出了一个基于量化压缩感测的通信高效联合学习框架。介绍的框架包括无线设备的梯度压缩和参数服务器(PS)的梯度重建。我们的梯度压缩战略是按顺序实施块的环状、维度减少和四分化。由于梯度的扩大和量化,我们的战略可以实现比一位梯度梯度压缩的更高压缩率。对于从PS的压缩信号中准确汇总本地梯度,我们提出了一个用于梯度重建的大约最低平均平方差(MMSE)法,使用预期-最大化通用即近距离通行(EM-GAMP)算法。假设Bernoulli Gaussian-mixture 战略是连续地执行块块块块的块状宽度,这种算法反复更新了本地梯度与压缩信号的差幅值。我们用Busggang 理论来综合压缩信号的本地梯度,然后将MISGE估计MER值(EM-MMMA) 的近似缩略度分析结果,我们用GIS-MIS-MA 演示的缩压式的缩略图则进行了对GL的缩压的模拟的缩略图。