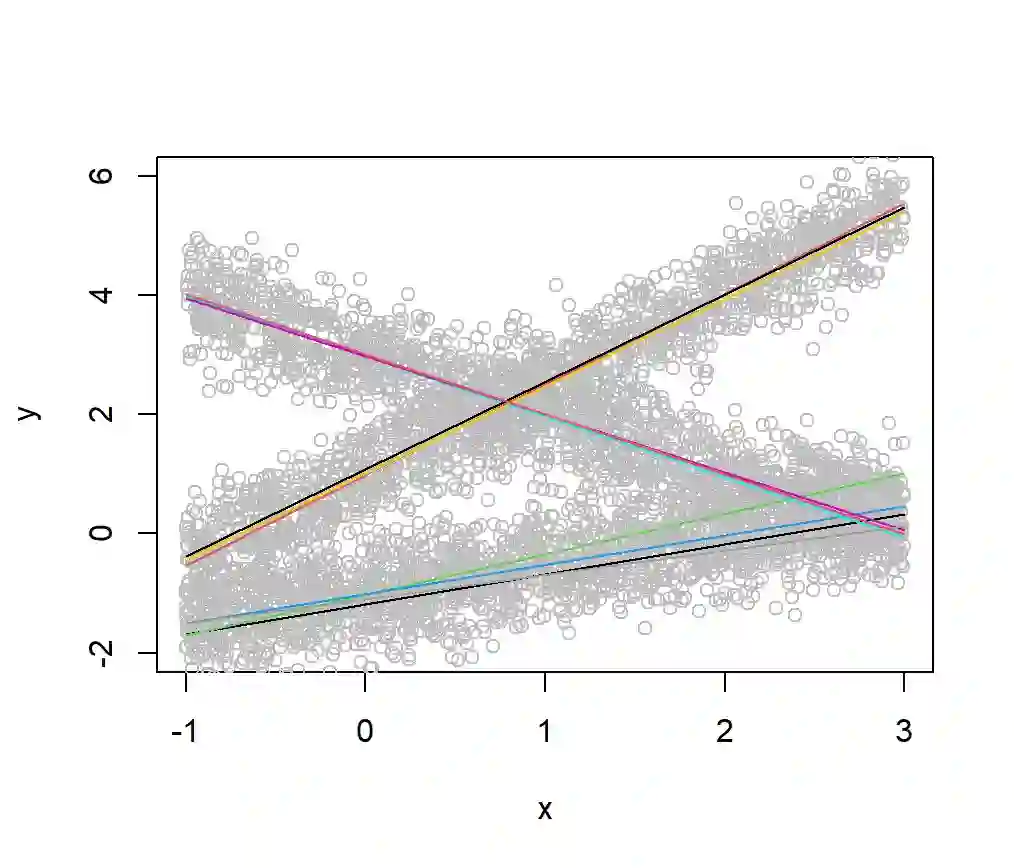
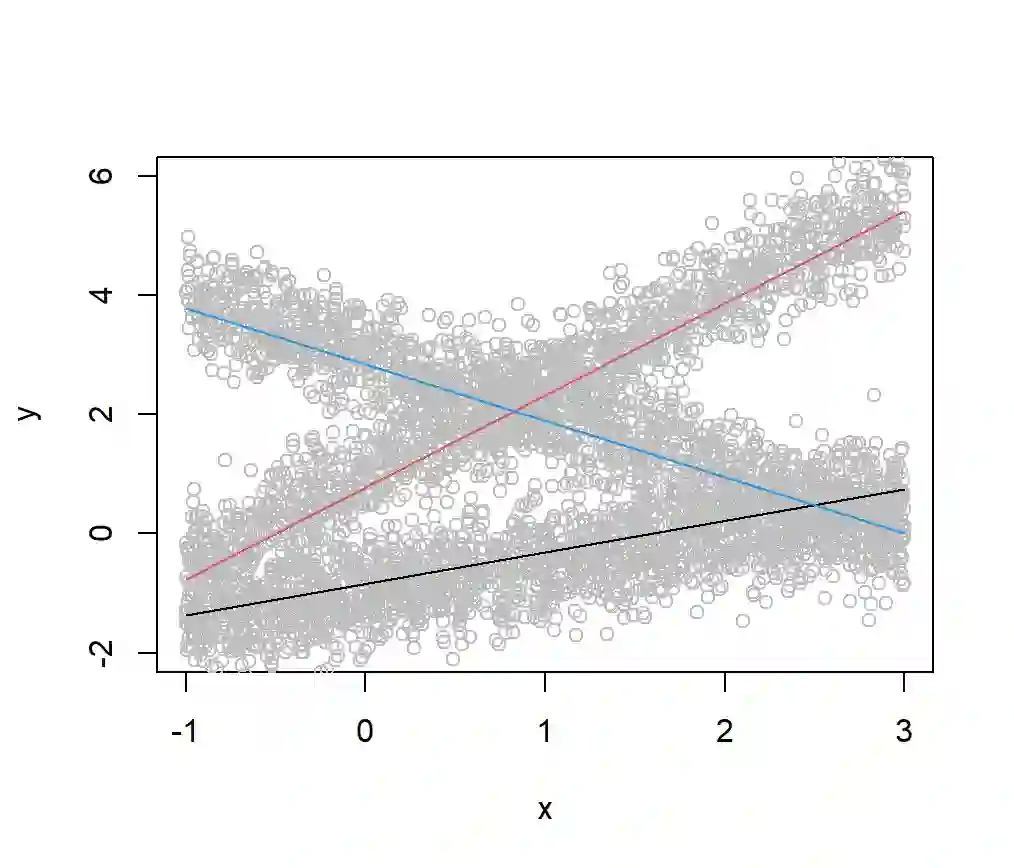
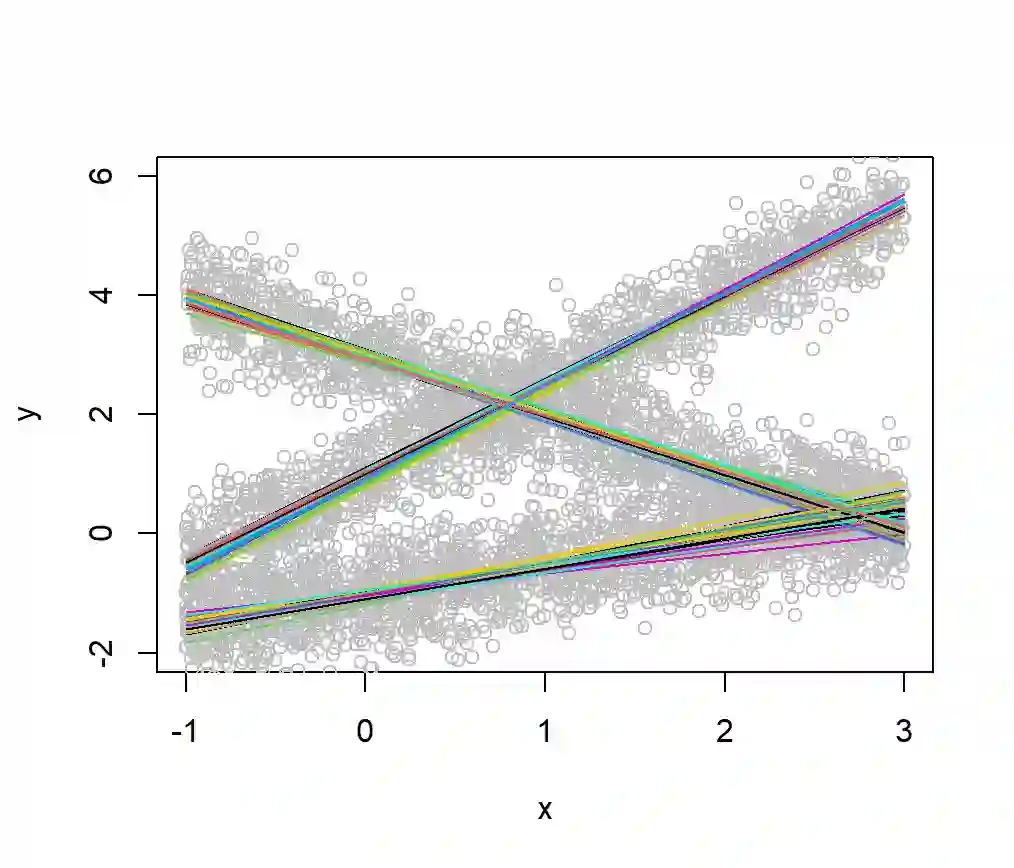
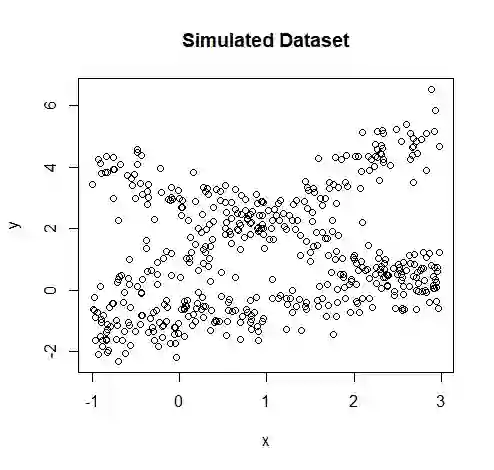
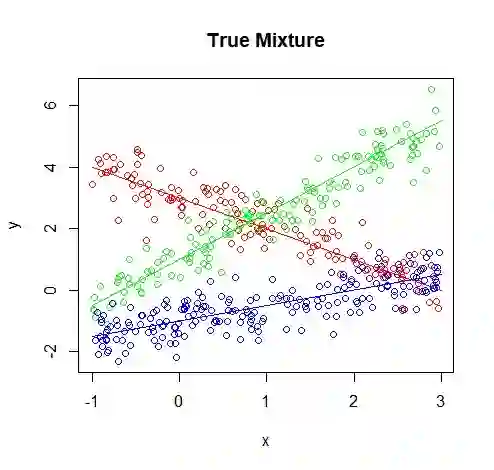
In a mixture of linear regression model, the regression coefficients are treated as random vectors that may follow either a continuous or discrete distribution. We propose two Expectation-Maximization (EM) algorithms to estimate this prior distribution. The first algorithm solves a kernelized version of the nonparametric maximum likelihood estimation (NPMLE). This method not only recovers continuous prior distributions but also accurately estimates the number of clusters when the prior is discrete. The second algorithm, designed to approximate the NPMLE, targets prior distributions with a density. It also performs well for discrete priors when combined with a post-processing step. We study the convergence properties of both algorithms and demonstrate their effectiveness through simulations and applications to real datasets.
翻译:在线性回归混合模型中,回归系数被视为可能服从连续或离散分布的随机向量。我们提出了两种期望最大化(EM)算法来估计该先验分布。第一种算法求解非参数最大似然估计(NPMLE)的核化版本。该方法不仅能恢复连续先验分布,还能在先验为离散时准确估计聚类数量。第二种算法旨在近似NPMLE,专门针对具有密度函数的先验分布。当结合后处理步骤时,该算法对离散先验同样表现良好。我们研究了两种算法的收敛性质,并通过仿真实验和真实数据集应用验证了其有效性。