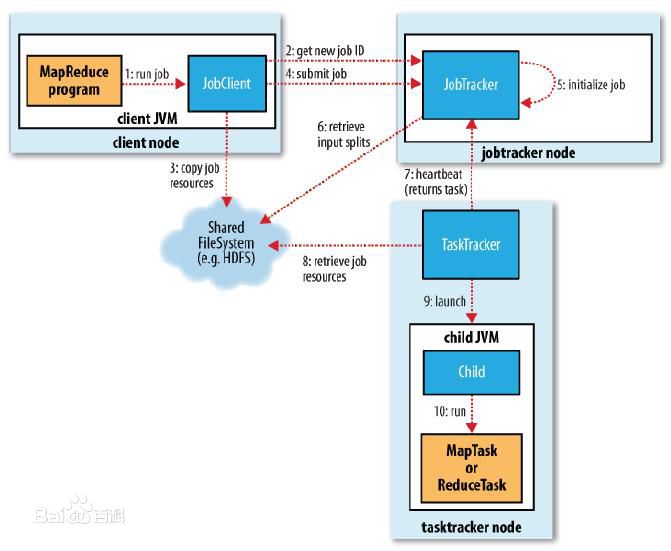
A multiple server setting is considered, where each server has tunable speed, and increasing the speed incurs an energy cost. Jobs arrive to a single queue, and each job has two types of sub-tasks, map and reduce, and a {\bf precedence} constraint among them: any reduce task of a job can only be processed once all the map tasks of the job have been completed. In addition to the scheduling problem, i.e., which task to execute on which server, with tunable speed, an additional decision variable is the choice of speed for each server, so as to minimize a linear combination of the sum of the flow times of jobs/tasks and the total energy cost. The precedence constraints present new challenges for the speed scaling problem with multiple servers, namely that the number of tasks that can be executed at any time may be small but the total number of outstanding tasks might be quite large. We present simple speed scaling algorithms that are shown to have competitive ratios, that depend on the power cost function, and/or the ratio of the size of the largest task and the shortest reduce task, but not on the number of jobs, or the number of servers.
翻译:考虑多个服务器设置, 每个服务器都具有缓冲速度, 并增加速度, 从而产生能量成本。 工作到达一个队列, 每个工作都有两种子任务类型, 地图和缩小, 以及 {bfserp} 的制约: 任务的任何缩减任务只能在全部任务完成之后才能处理 。 除了调度问题之外, 即执行哪个服务器的任务, 以缓冲速度, 额外的决定变量是每个服务器的速度选择, 以便尽可能减少任务/ 任务流时间和总能源成本的总和的线性组合 。 优先限制对多个服务器的速度缩放问题提出了新的挑战, 即任何时候可以执行的任务数量可能很小, 但未完成的任务总数可能相当大 。 我们展示的简单速度缩放算算法显示具有竞争性比率, 取决于电力成本功能, 和/ 最大任务规模和最短任务的比例, 但不取决于工作数量, 或服务器数量 。