Dynamic inference in probabilistic graphical models

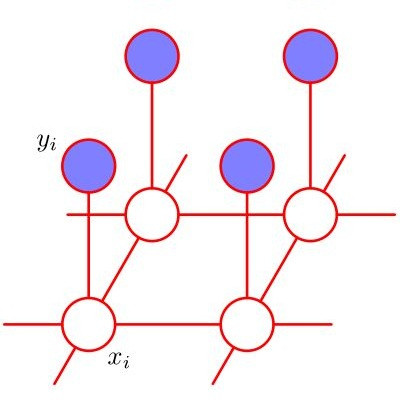
Probabilistic graphical models, such as Markov random fields (MRFs), are useful for describing high-dimensional distributions in terms of local dependence structures. The probabilistic inference is a fundamental problem related to graphical models, and sampling is a main approach for the problem. In this paper, we study probabilistic inference problems when the graphical model itself is changing dynamically with time. Such dynamic inference problems arise naturally in today's application, e.g.~multivariate time-series data analysis and practical learning procedures. We give a dynamic algorithm for sampling-based probabilistic inferences in MRFs, where each dynamic update can change the underlying graph and all parameters of the MRF simultaneously, as long as the total amount of changes is bounded. More precisely, suppose that the MRF has $n$ variables and polylogarithmic-bounded maximum degree, and $N(n)$ independent samples are sufficient for the inference for a polynomial function $N(\cdot)$. Our algorithm dynamically maintains an answer to the inference problem using $\widetilde{O}(n N(n))$ space cost, and $\widetilde{O}(N(n) + n)$ incremental time cost upon each update to the MRF, as long as the well-known Dobrushin-Shlosman condition is satisfied by the MRFs. Compared to the static case, which requires $\Omega(n N(n))$ time cost for redrawing all $N(n)$ samples whenever the MRF changes, our dynamic algorithm gives a $\widetilde\Omega(\min\{n, N(n)\})$-factor speedup. Our approach relies on a novel dynamic sampling technique, which transforms local Markov chains (a.k.a. single-site dynamics) to dynamic sampling algorithms, and an "algorithmic Lipschitz" condition that we establish for sampling from graphical models, namely, when the MRF changes by a small difference, samples can be modified to reflect the new distribution, with cost proportional to the difference on MRF.