Error estimates of the time-splitting methods for the nonlinear {S}chrödinger equation with semi-smooth nonlinearity

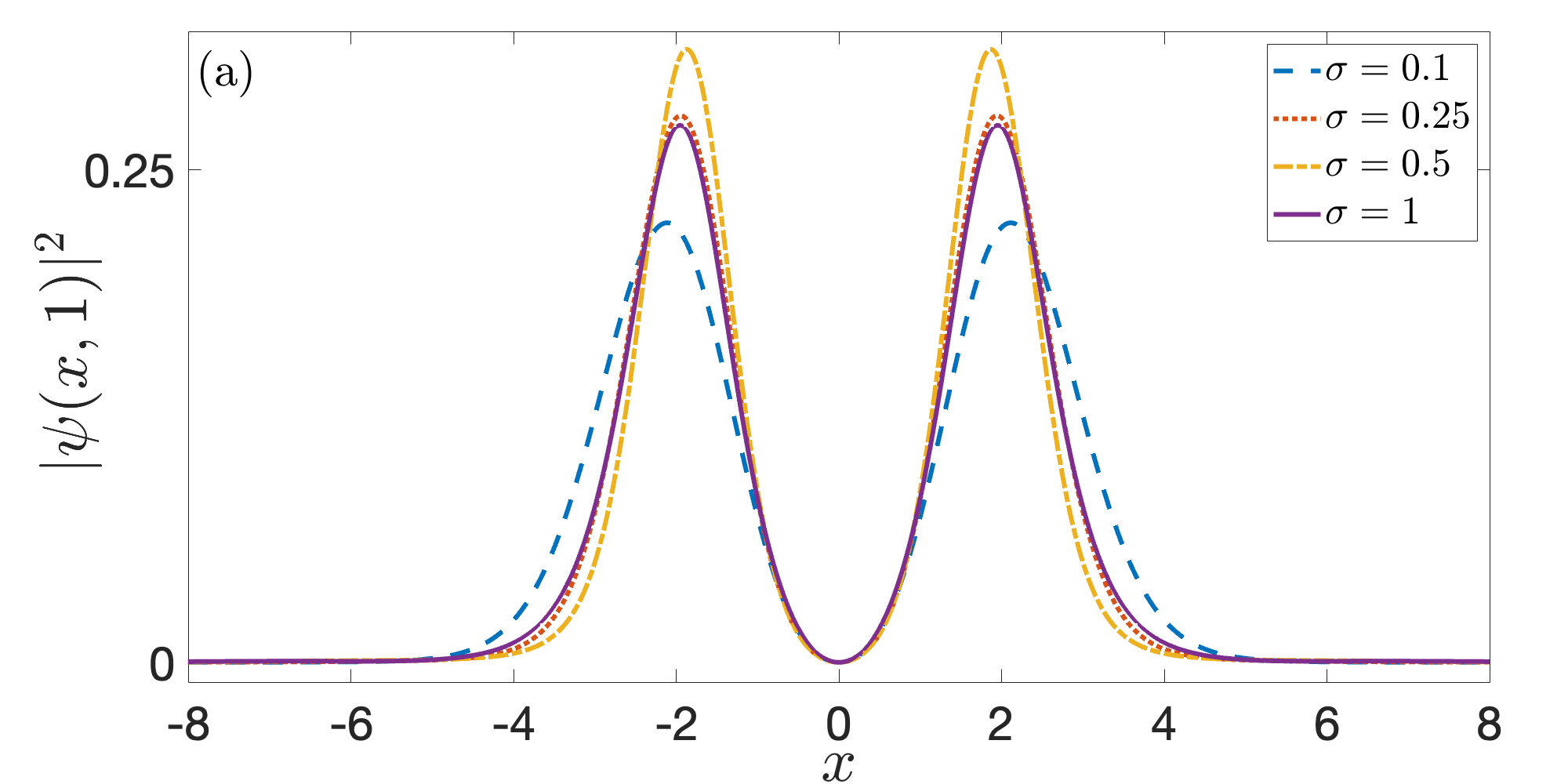
We establish error bounds of the Lie-Trotter time-splitting sine pseudospectral method for the nonlinear Schr\"odinger equation (NLSE) with semi-smooth nonlinearity $ f(\rho) = \rho^\sigma$, where $\rho=|\psi|^2$ is the density with $\psi$ the wave function and $\sigma>0$ is the exponent of the semi-smooth nonlinearity. Under the assumption of $ H^2 $-solution of the NLSE, we prove error bounds at $ O(\tau^{\frac{1}{2}+\sigma} + h^{1+2\sigma}) $ and $ O(\tau + h^{2}) $ in $ L^2 $-norm for $0<\sigma\leq\frac{1}{2}$ and $\sigma\geq\frac{1}{2}$, respectively, and an error bound at $ O(\tau^\frac{1}{2} + h) $ in $ H^1 $-norm for $\sigma\geq \frac{1}{2}$, where $h$ and $\tau$ are the mesh size and time step size, respectively. In addition, when $\frac{1}{2}<\sigma<1$ and under the assumption of $ H^3 $-solution of the NLSE, we show an error bound at $ O(\tau^{\sigma} + h^{2\sigma}) $ in $ H^1 $-norm. Two key ingredients are adopted in our proof: one is to adopt an unconditional $ L^2 $-stability of the numerical flow in order to avoid an a priori estimate of the numerical solution for the case of $ 0 < \sigma \leq \frac{1}{2}$, and to establish an $ l^\infty $-conditional $ H^1 $-stability to obtain the $ l^\infty $-bound of the numerical solution by using the mathematical induction and the error estimates for the case of $ \sigma \ge \frac{1}{2}$; and the other one is to introduce a regularization technique to avoid the singularity of the semi-smooth nonlinearity in obtaining improved local truncation errors. Finally, numerical results are reported to demonstrate our error bounds.