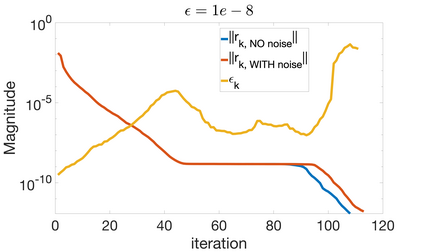
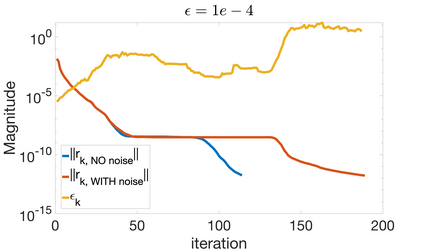
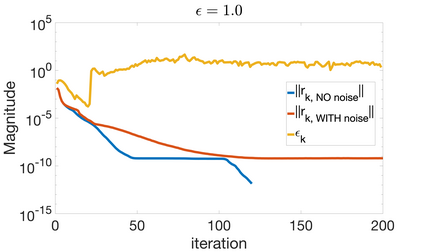
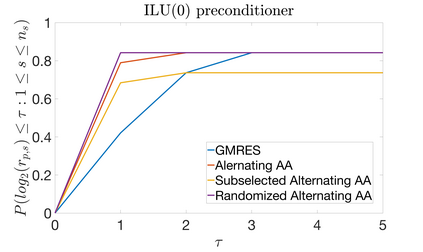
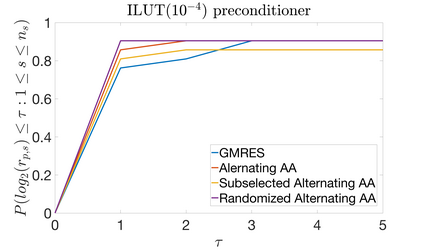
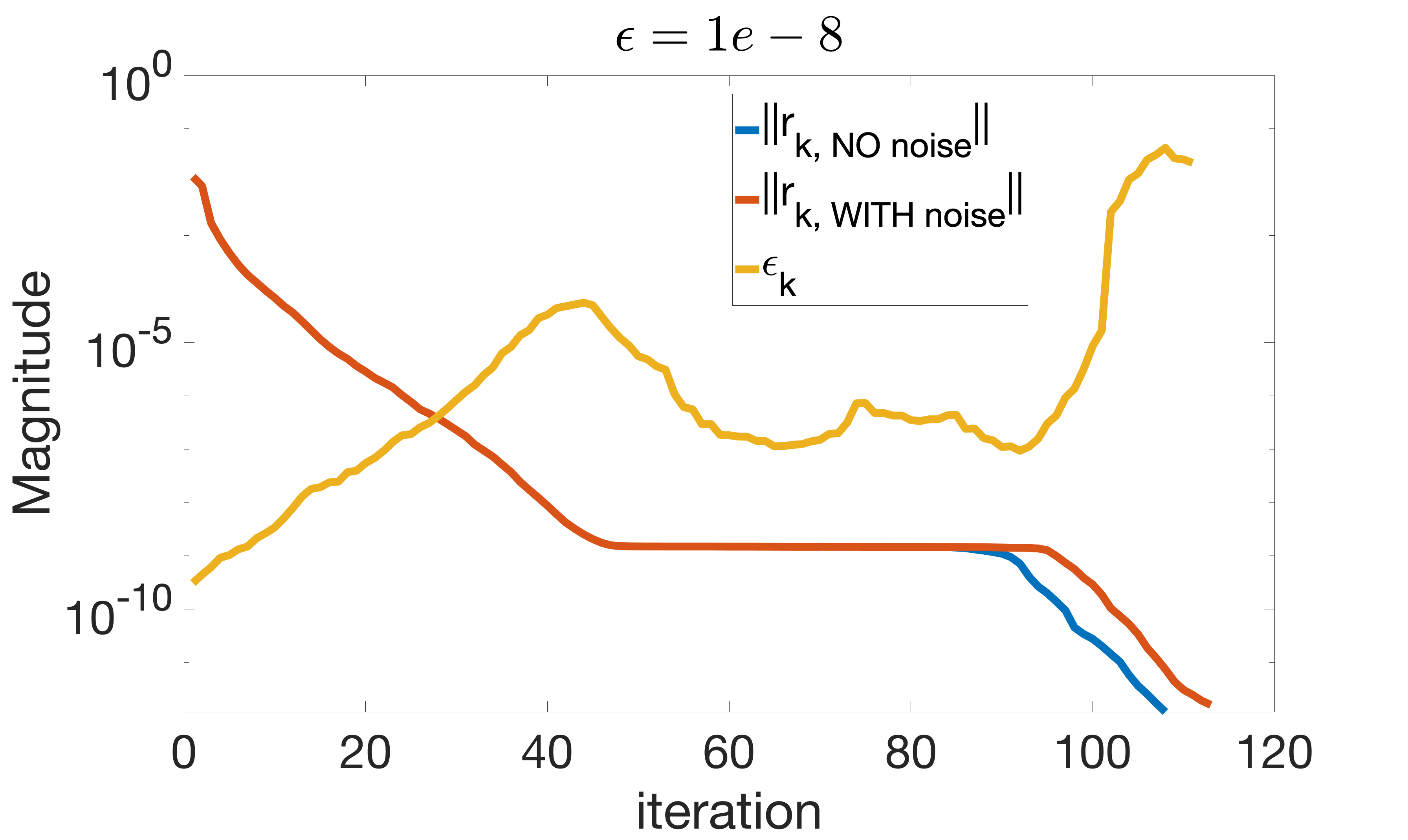
We provide rigorous theoretical bounds for Anderson acceleration (AA) that allow for efficient approximate calculations of the residual, which reduce computational time and memory storage while maintaining convergence. Specifically, we propose a reduced variant of AA, which consists in projecting the least squares to compute the Anderson mixing onto a subspace of reduced dimension. The dimensionality of this subspace adapts dynamically at each iteration as prescribed by computable heuristic quantities guided by the theoretical error bounds. The use of the heuristic to monitor the error introduced by approximate calculations, combined with the check on monotonicity of the convergence, ensures the convergence of the numerical scheme within a prescribed tolerance threshold on the residual. We numerically assess the performance of AA with approximate calculations on: (i) linear deterministic fixed-point iterations arising from the Richardson's scheme to solve linear systems with open-source benchmark matrices with various preconditioners and (ii) non-linear deterministic fixed-point iterations arising from non-linear time-dependent Boltzmann equations.
翻译:我们为安德森加速(AA)提供了严格的理论界限,允许对残留物进行有效的近似计算,从而减少计算时间和内存存储,同时保持趋同。具体地说,我们提议减少AA的变方,即预测最小方形,以计算安德森混合到一个降低尺寸的子空间。这个子空间的维度根据理论误差界限指导的计算超强数量,动态地适应每个迭代。使用超量来监测通过近似计算带来的错误,同时检查趋同的单一性,确保数字方法在残留物规定的容忍阈值内趋同。我们从数字上评估AA的性能,并大致计算到:(一) 里查森用各种先决条件和(二) 非线性确定性定点定点定点定点等式解决开源基准矩阵的线性系统所产生的线性定点迭代。