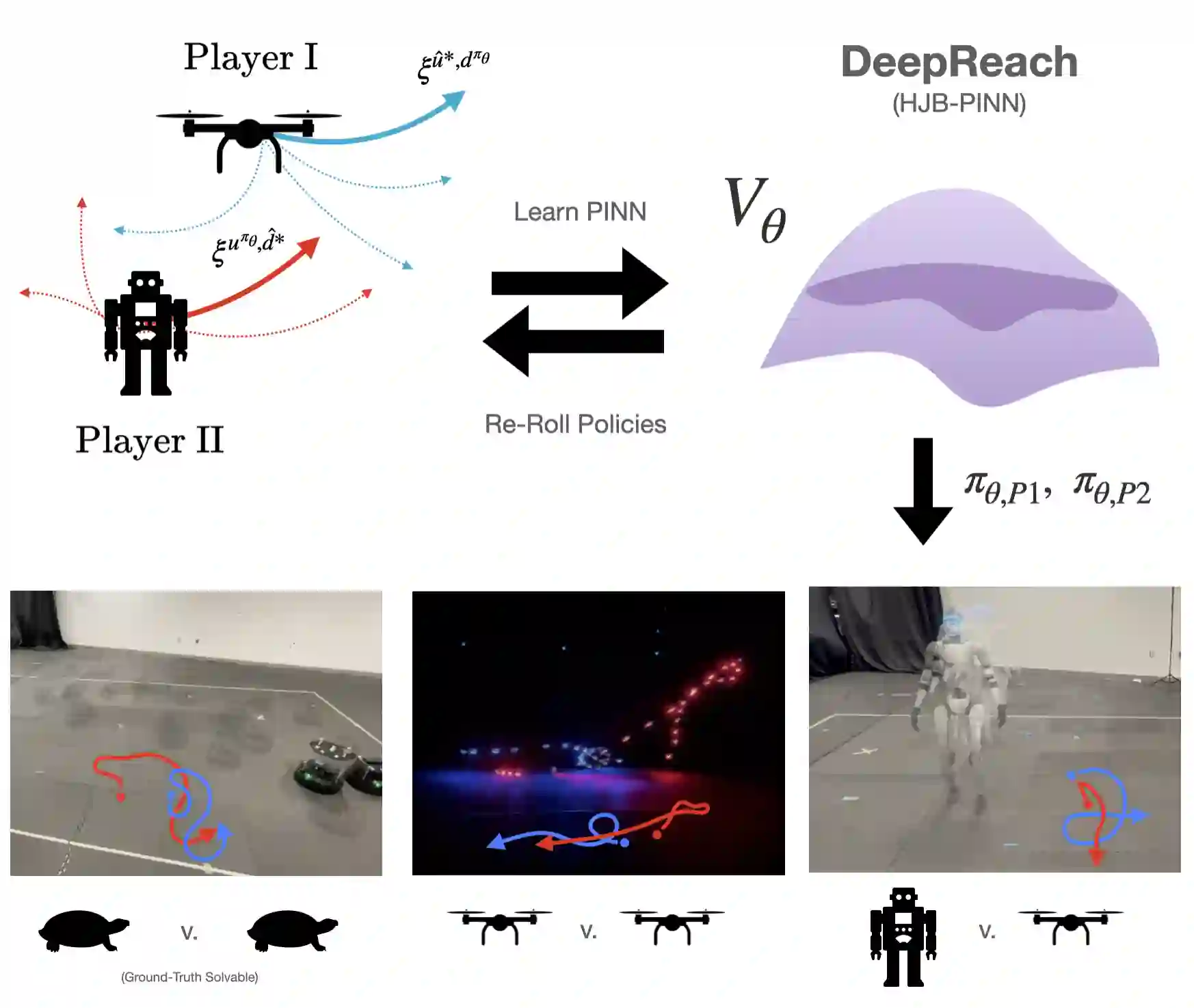
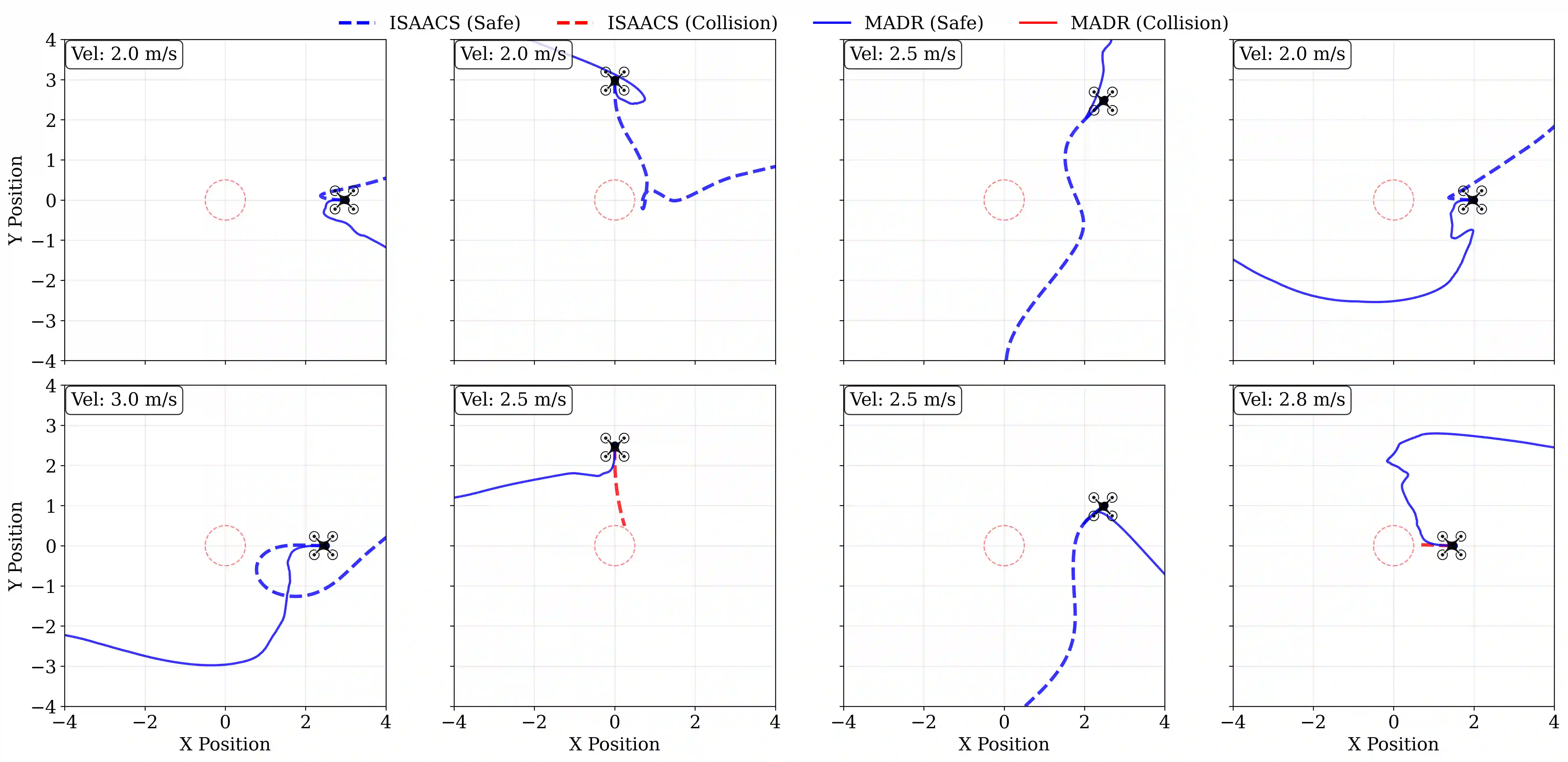
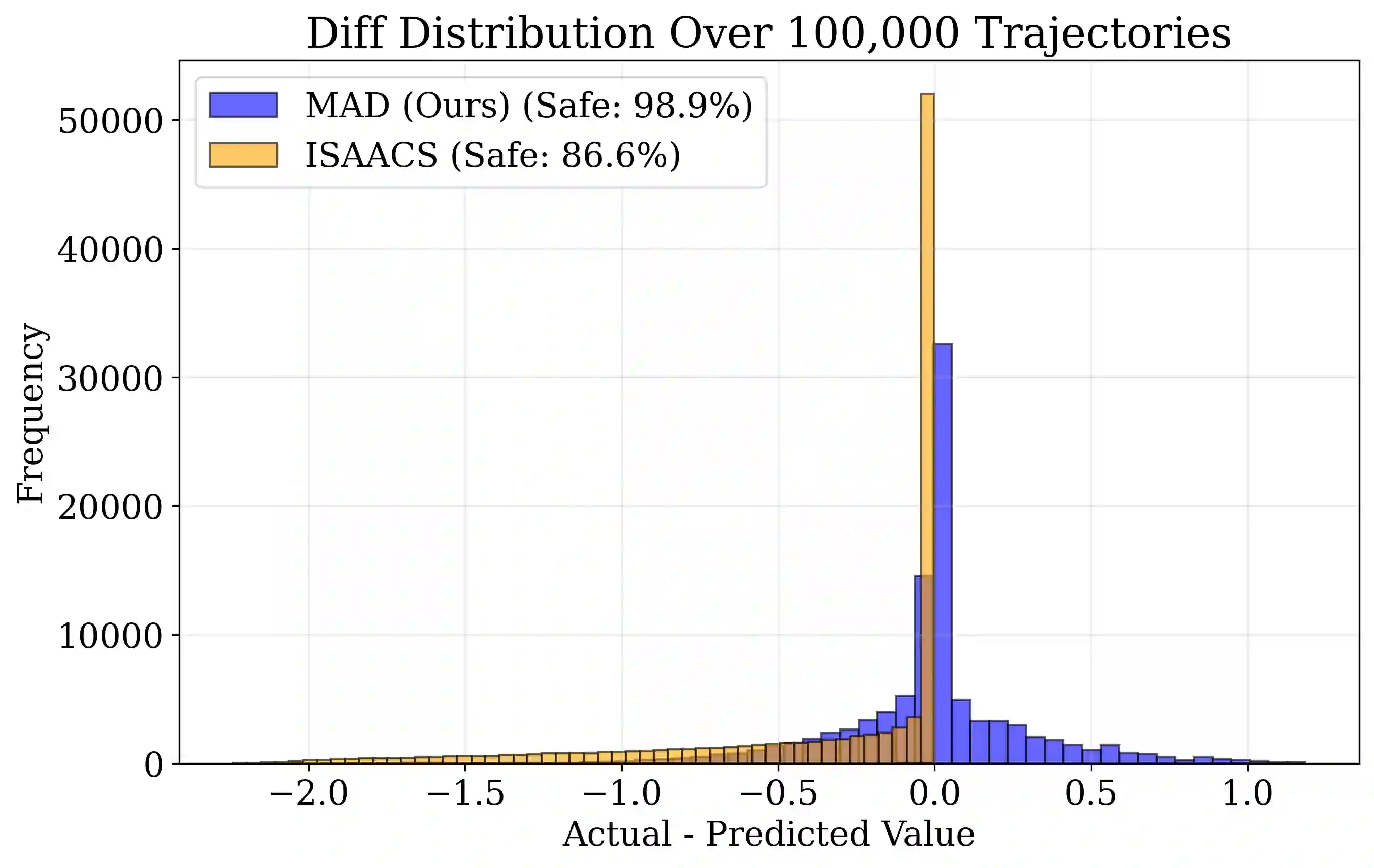
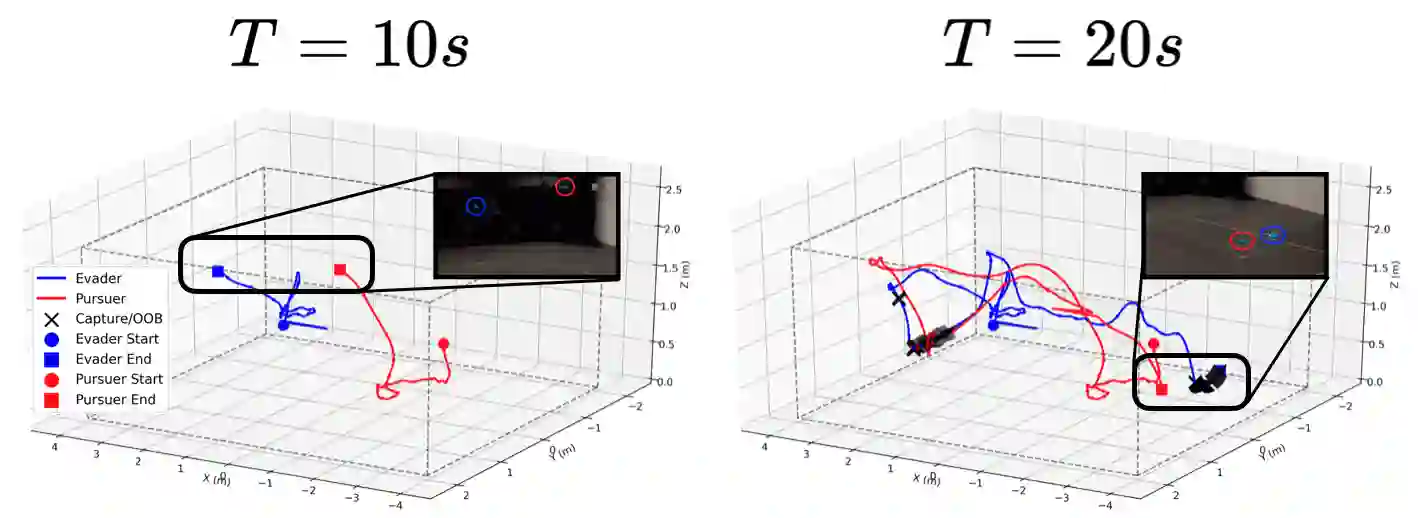
Hamilton-Jacobi (HJ) Reachability offers a framework for generating safe value functions and policies in the face of adversarial disturbance, but is limited by the curse of dimensionality. Physics-informed deep learning is able to overcome this infeasibility, but itself suffers from slow and inaccurate convergence, primarily due to weak PDE gradients and the complexity of self-supervised learning. A few works, recently, have demonstrated that enriching the self-supervision process with regular supervision (based on the nature of the optimal control problem), greatly accelerates convergence and solution quality, however, these have been limited to single player problems and simple games. In this work, we introduce MADR: MPC-guided Adversarial DeepReach, a general framework to robustly approximate the two-player, zero-sum differential game value function. In doing so, MADR yields the corresponding optimal strategies for both players in zero-sum games as well as safe policies for worst-case robustness. We test MADR on a multitude of high-dimensional simulated and real robotic agents with varying dynamics and games, finding that our approach significantly out-performs state-of-the-art baselines in simulation and produces impressive results in hardware.
翻译:汉密尔顿-雅可比(HJ)可达性分析为在对抗性扰动下生成安全值函数与策略提供了理论框架,但其受限于维度灾难问题。基于物理信息的深度学习能够克服这一计算不可行性,但其自身存在收敛速度慢且精度不足的问题,主要源于偏微分方程梯度的弱监督特性及自监督学习的复杂性。近期少数研究表明,通过融入基于最优控制问题本质的常规监督来增强自监督过程,能显著提升收敛速度与解的质量,但这些研究仅限于单智能体问题及简单博弈场景。本文提出MADR:MPC引导的对抗性深度可达性方法,该通用框架能够鲁棒地逼近双人零和微分博弈的值函数。通过此方法,MADR可同时导出零和博弈中双方参与者的最优策略,以及最坏情况鲁棒性下的安全策略。我们在多种具有不同动力学特性和博弈场景的高维仿真与真实机器人智能体上测试MADR,结果表明该方法在仿真中显著优于现有先进基线,并在硬件实验中取得了令人瞩目的效果。