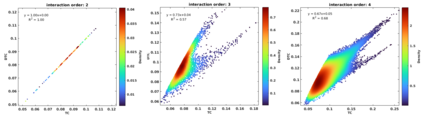
Pairwise metrics are often employed to estimate statistical dependencies between brain regions, however they do not capture higher-order information interactions. It is critical to explore higher-order interactions that go beyond paired brain areas in order to better understand information processing in the human brain. To address this problem, we applied multivariate mutual information, specifically, Total Correlation and Dual Total Correlation to reveal higher-order information in the brain. In this paper, we estimate these metrics using matrix-based R\'enyi's entropy, which offers a direct and easily interpretable approach that is not limited by direct assumptions about probability distribution functions of multivariate time series. We applied these metrics to resting-state fMRI data in order to examine higher-order interactions in the brain. Our results showed that the higher-order information interactions captured increase gradually as the interaction order increases. Furthermore, we observed a gradual increase in the correlation between the Total Correlation and Dual Total Correlation as the interaction order increased. In addition, the significance of Dual Total Correlation values compared to Total Correlation values also indicate that the human brain exhibits synergy dominance during the resting state.
翻译:人脑区域之间的统计依赖通常使用成对的度量来估计,但这并不能捕捉更高阶的信息交互。探索高阶信息交互对于更好地理解人脑信息处理至关重要。为了解决这个问题,我们应用了多变量互信息, 特别是全相关和对偶全相关以揭示人脑中的高阶信息。在本文中,我们使用基于瑞尼(Renyi)熵的矩阵方法来估计这些度量,这种方法提供了一种直接且易于解释的方法,不受多元时间序列概率分布函数的直接假设的限制。我们将这些度量应用于静息态fMRI数据以研究人脑的高阶交互。我们的结果表明, 随着交互阶数的增加,所捕捉到的高阶信息交互逐渐增加。此外,我们还观察到对偶全相关和全相关之间的相关性随着交互阶数的增加而逐渐增加。另外,对偶全相关值与全相关值之间的显著性,也表明人脑在静息状态下呈现出协同优势。