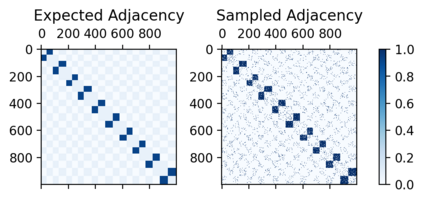
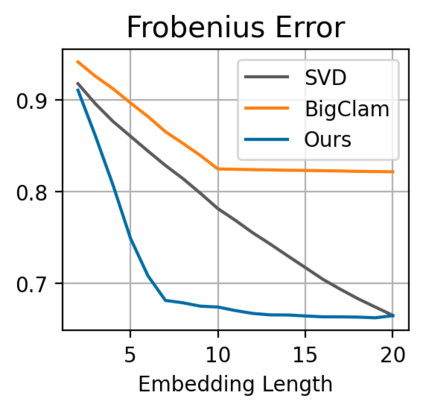
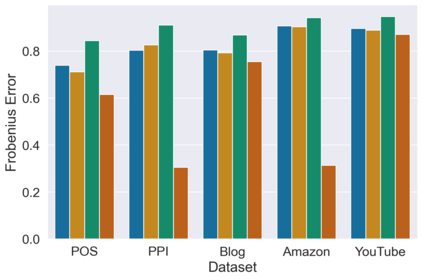
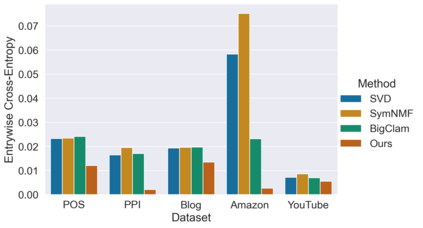
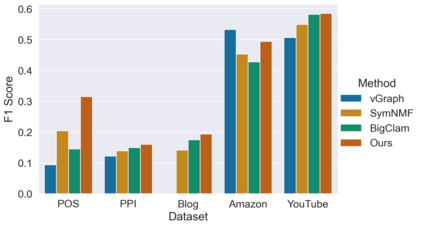
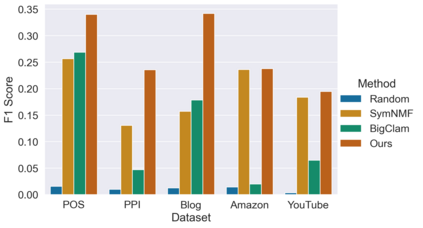
Many models for graphs fall under the framework of edge-independent dot product models. These models output the probabilities of edges existing between all pairs of nodes, and the probability of a link between two nodes increases with the dot product of vectors associated with the nodes. Recent work has shown that these models are unable to capture key structures in real-world graphs, particularly heterophilous structures, wherein links occur between dissimilar nodes. We propose the first edge-independent graph generative model that is a) expressive enough to capture heterophily, b) produces nonnegative embeddings, which allow link predictions to be interpreted in terms of communities, and c) optimizes effectively on real-world graphs with gradient descent on a cross-entropy loss. Our theoretical results demonstrate the expressiveness of our model in its ability to exactly reconstruct a graph using a number of clusters that is linear in the maximum degree, along with its ability to capture both heterophily and homophily in the data. Further, our experiments demonstrate the effectiveness of our model for a variety of important application tasks such as multi-label clustering and link prediction.
翻译:许多图表模型都属于边缘独立的点产品模型的框架。 这些模型输出出所有节点之间现有边缘的概率, 以及两个节点之间联系的可能性随着节点相关矢量的点产物而增加。 最近的工作表明, 这些模型无法捕捉真实世界图形中的关键结构, 特别是异端节点之间有联系的异性嗜血结构。 我们提议第一个边缘独立的图形基因模型, 其表达方式足以捕捉异性, b) 产生非负性嵌入, 从而能够用社区来解释链接的预测, c) 优化现实世界图中带有跨热带损失的梯度下降的优化。 我们的理论结果表明,我们模型在利用最大程度为线性的若干集群来精确重建图表的能力, 以及它在数据中既能捕捉异性和同性两种特性的能力。 此外, 我们的实验还展示了我们模型在一系列重要应用任务上的有效性, 如多标签群链接和多标签链接。