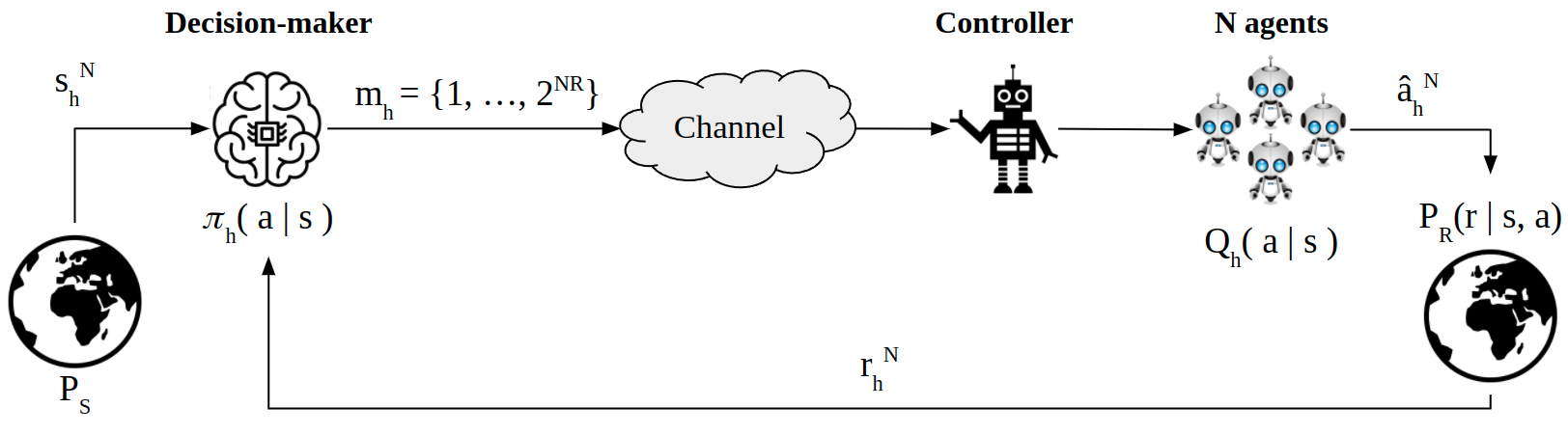
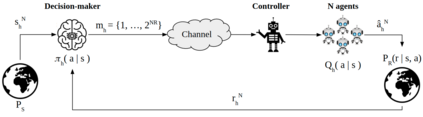
We consider a remote contextual multi-armed bandit (CMAB) problem, in which the decision-maker observes the context and the reward, but must communicate the actions to be taken by the agents over a rate-limited communication channel. This can model, for example, a personalized ad placement application, where the content owner observes the individual visitors to its website, and hence has the context information, but must convey the ads that must be shown to each visitor to a separate entity that manages the marketing content. In this remote CMAB (R-CMAB) problem, the constraint on the communication rate between the decision-maker and the agents imposes a trade-off between the number of bits sent per agent and the acquired average reward. We are particularly interested in characterizing the rate required to achieve sub-linear regret. Consequently, this can be considered as a policy compression problem, where the distortion metric is induced by the learning objectives. We first study the fundamental information theoretic limits of this problem by letting the number of agents go to infinity, and study the regret achieved when Thompson sampling strategy is adopted. In particular, we identify two distinct rate regions resulting in linear and sub-linear regret behavior, respectively. Then, we provide upper bounds on the achievable regret when the decision-maker can reliably transmit the policy without distortion.
翻译:我们考虑的是远程背景多武装匪盗(CMAB)问题,在这一问题中,决策者观察背景和奖励,但必须通报代理人在受费率限制的通信渠道中应采取的行动。例如,这可以模拟个性化广告申请,内容所有者观察访问其网站的个人访问者,因此有背景信息,但必须将必须向每个访问者展示的广告传达给管理营销内容的单独实体。在这个偏远的CMAB(R-CMAB)问题中,决策者和代理人之间通信率的制约因素使每个代理人发送的比特数与获得的平均奖励之间的平衡。例如,我们特别感兴趣的是确定实现亚线性遗憾所需的比例。因此,这可以被视为一个政策压缩问题,因为扭曲的衡量标准是由学习目标引起的。我们首先研究这一问题的基本信息,让代理人的数量变得无限,并研究在采用汤普森取样战略时所实现的遗憾。特别是,我们确定两个不同的比例区域,分别导致直线式和子线式决策师的升级,然后提供可实现的后期政策。