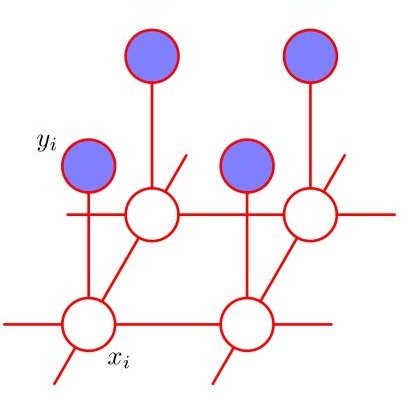
We introduce a probabilistic formalism subsuming Markov random fields of bounded tree width and probabilistic context free grammars. Our models are based on a representation of Boolean formulas that we call case-factor diagrams (CFDs). CFDs are similar to binary decision diagrams (BDDs) but are concise for circuits of bounded tree width (unlike BDDs) and can concisely represent the set of parse trees over a given string undera given context free grammar (also unlike BDDs). A probabilistic model consists of aCFD defining a feasible set of Boolean assignments and a weight (or cost) for each individual Boolean variable. We give an insideoutside algorithm for simultaneously computing the marginal of each Boolean variable, and a Viterbi algorithm for finding the mininum cost variable assignment. Both algorithms run in time proportional to the size of the CFD.
翻译:我们引入了一种概率化的形式主义, 以连接树宽度和概率背景自由语法的马可夫随机字段为代表。 我们的模型基于一种布林公式的表达方式, 我们称之为案件因子图( CFDs ) 。 CFD 类似于二进制决定图( BDDs ), 但对于连接树宽度的电路( 与 BDDs 不同 ), 简洁地代表给定字符串底线上一组粗糙的树( 与 BDDs 不同 ) 。 一种概率模型由一个 CFD 构成, 定义一套可行的布林任务和每个单个布林变量的重量( 或成本 ) 。 我们给出了一种内部算法, 用于同时计算每个布林变量的边际值, 以及 寻找最小核成本变量的 Viterbi 算法。 这两种算法都与 CDFD 的大小成比例。