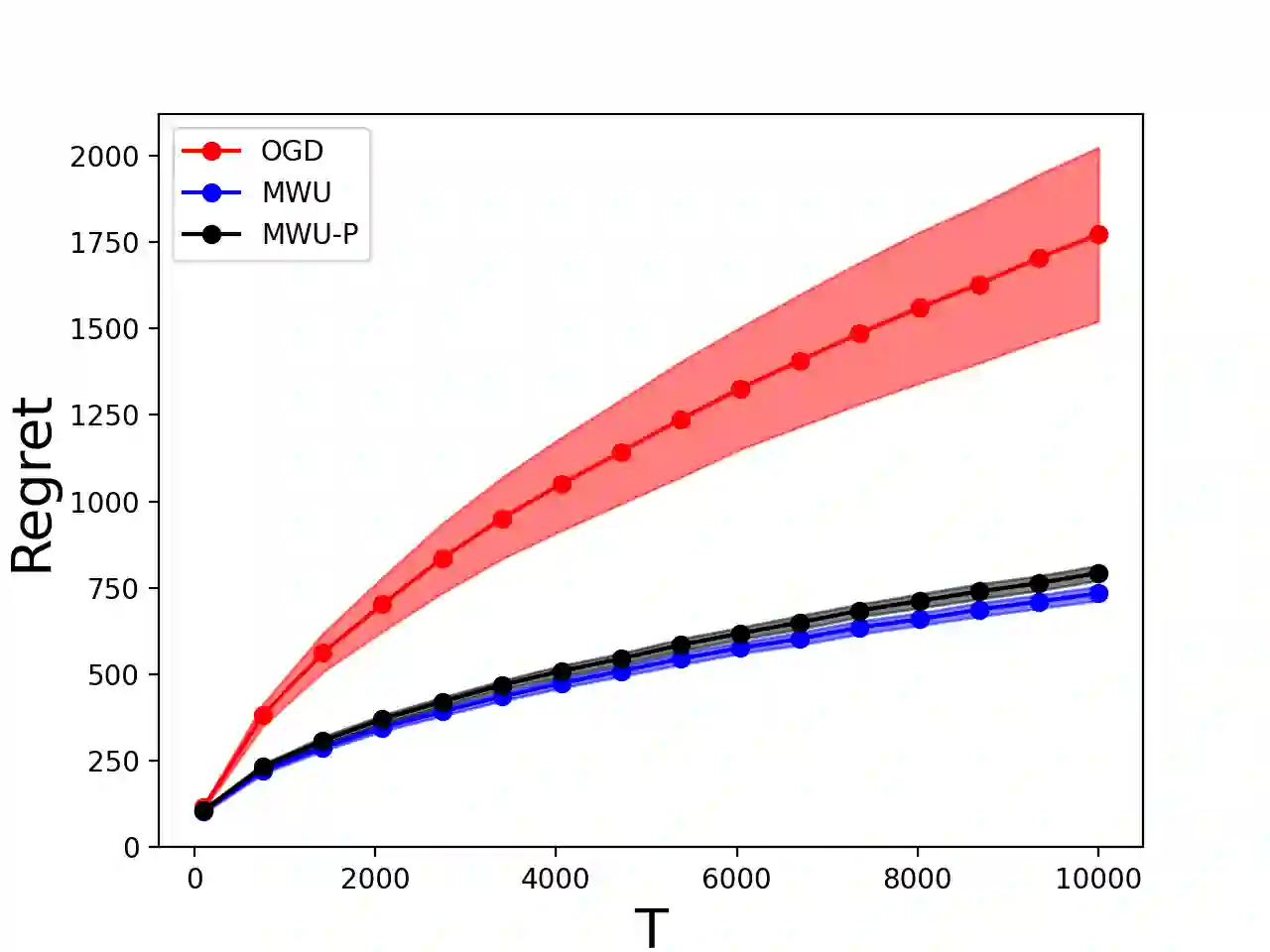
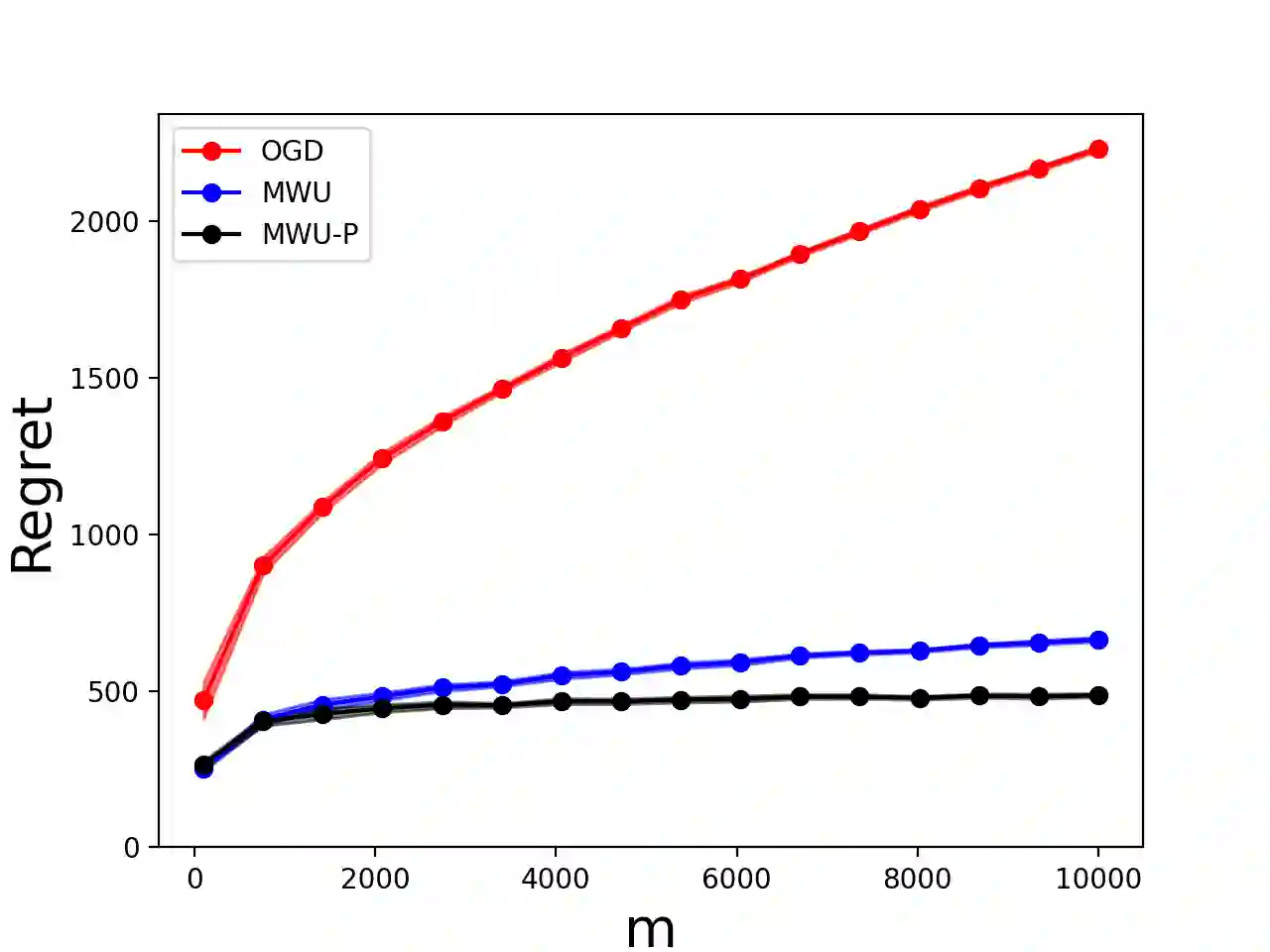
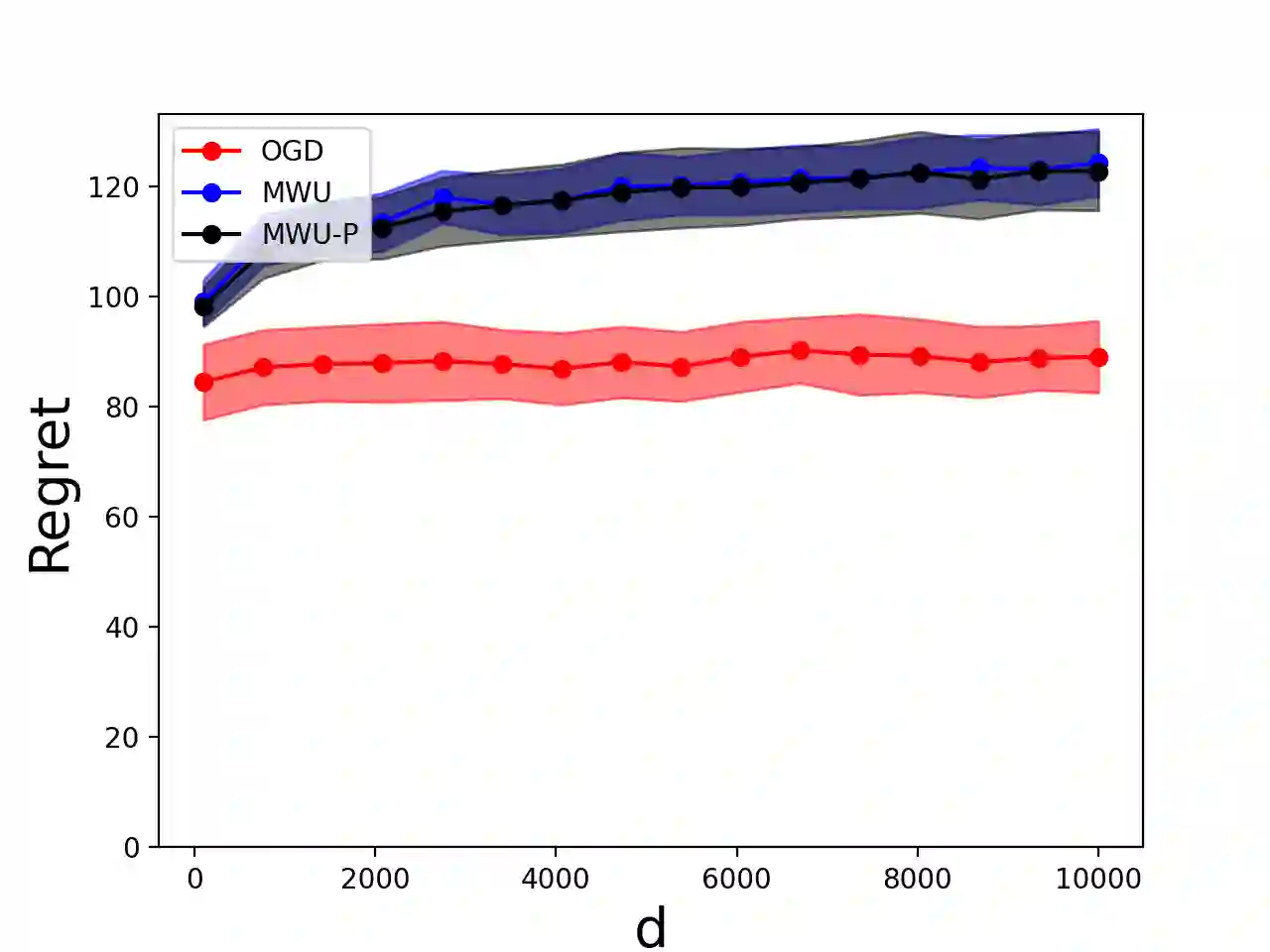
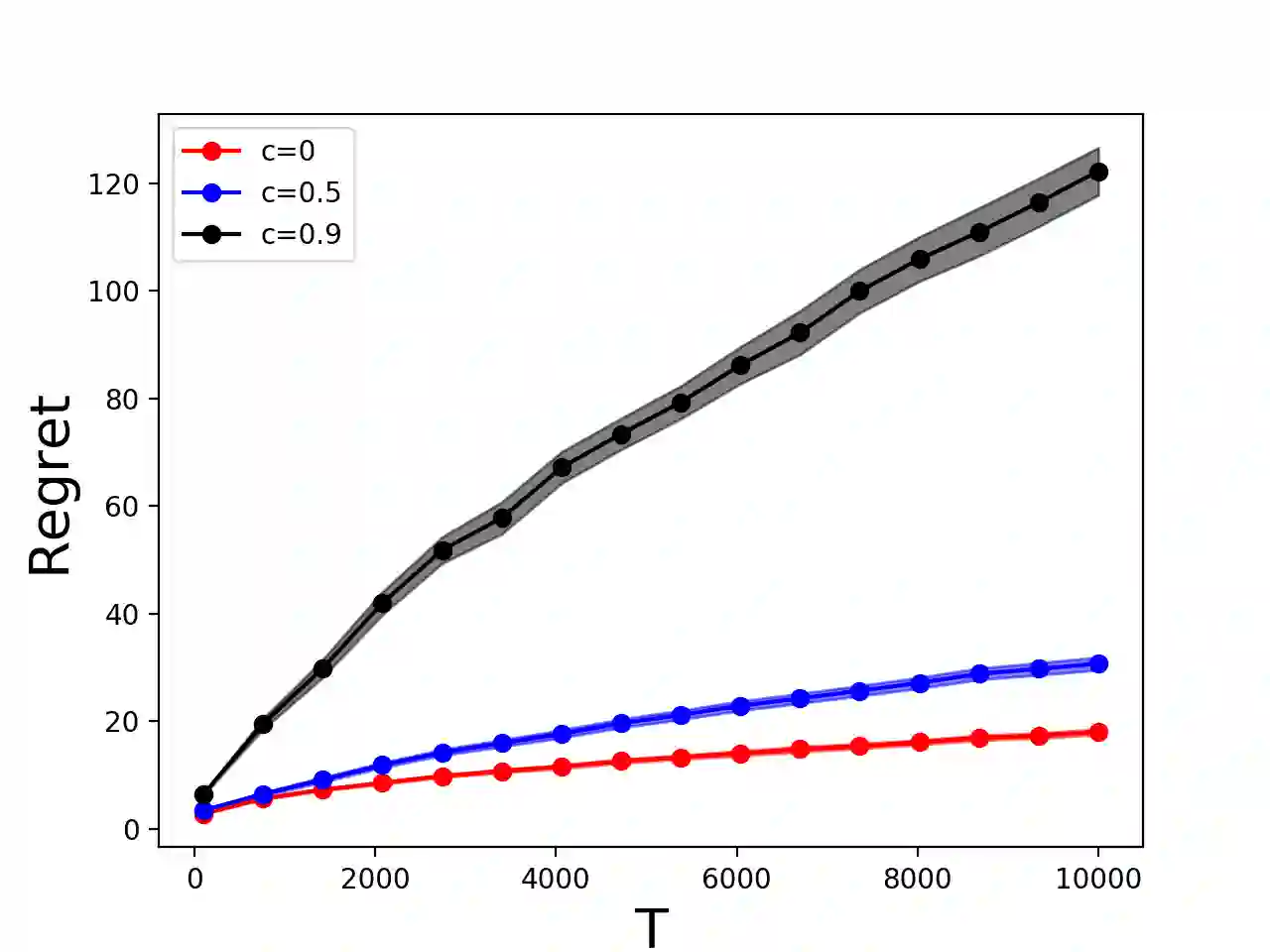
Online allocation problems with resource constraints are central problems in revenue management and online advertising. In these problems, requests arrive sequentially during a finite horizon and, for each request, a decision maker needs to choose an action that consumes a certain amount of resources and generates reward. The objective is to maximize cumulative rewards subject to a constraint on the total consumption of resources. In this paper, we consider a data-driven setting in which the reward and resource consumption of each request are generated using an input model that is unknown to the decision maker. We design a general class of algorithms that attain good performance in various inputs models without knowing which type of input they are facing. In particular, our algorithms are asymptotically optimal under stochastic i.i.d. input model as well as various non-stationary stochastic input models, and they attain an asymptotically optimal fixed competitive ratio when the input is adversarial. Our algorithms operate in the Lagrangian dual space: they maintain a dual multiplier for each resource that is updated using online mirror descent. By choosing the reference function accordingly, we recover dual sub-gradient descent and dual exponential weights algorithm. The resulting algorithms are simple, fast, and have minimal requirements on the reward functions, consumption functions and the action space, in contrast to existing methods for online allocation problems. We discuss applications to network revenue management, online bidding in repeated auctions with budget constraints, online proportional matching with high entropy, and personalized assortment optimization with limited inventories.
翻译:资源限制的在线分配问题是收入管理和在线广告方面的中心问题。在这些问题上,请求是按顺序在一定的视野内收到的,对于每项请求,决策者需要选择一种消耗一定数量的资源并产生奖赏的行动。目标是在资源消耗总量受限制的情况下最大限度地累积奖励。在本文中,我们考虑一种由数据驱动的环境,即每项请求的奖赏和资源消耗是使用决策者所不知道的投入模式产生的一种输入模式产生的。我们设计了一种一般的算法,这种算法在各种投入模式中取得良好业绩,而不知道它们所面临的是何种投入类型。特别是,我们的算法在Stochchatical i.i.d.d.下是尽可能最佳的。目标是在投入是对抗性的情况下,最大限度地实现累积性固定的竞争比率。 我们的算法在Lagrangian的双重空间运行:对每项资源都保持一种双倍的乘数,而没有了解它们所面临的投入模式。我们选择的参考功能,因此,我们的算法是双重的次等最佳最佳最佳最佳最佳选择方法, 以及在线计算,在快速的汇率和双向交易中,对等的计算。