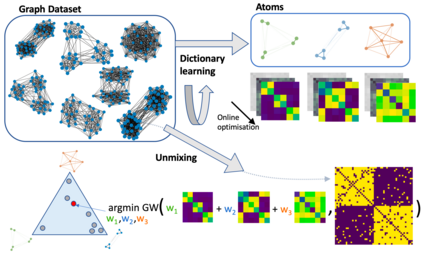
Dictionary learning is a key tool for representation learning, that explains the data as linear combination of few basic elements. Yet, this analysis is not amenable in the context of graph learning, as graphs usually belong to different metric spaces. We fill this gap by proposing a new online Graph Dictionary Learning approach, which uses the Gromov Wasserstein divergence for the data fitting term. In our work, graphs are encoded through their nodes' pairwise relations and modeled as convex combination of graph atoms, i.e. dictionary elements, estimated thanks to an online stochastic algorithm, which operates on a dataset of unregistered graphs with potentially different number of nodes. Our approach naturally extends to labeled graphs, and is completed by a novel upper bound that can be used as a fast approximation of Gromov Wasserstein in the embedding space. We provide numerical evidences showing the interest of our approach for unsupervised embedding of graph datasets and for online graph subspace estimation and tracking.
翻译:词典学习是代表学习的关键工具,它将数据解释为少数基本元素的线性组合。然而,这一分析在图形学习的背景下并不适合,因为图表通常属于不同的量空间。我们通过提出一个新的在线图形词典学习方法来填补这一空白,该方法在数据匹配术语中采用格罗莫夫·瓦西尔斯坦差异法。在我们的工作中,图表通过结点的双向关系进行编码,并以图形原子(即字典元素)的二次组合模型来建模。由于在线的随机算法而估算,该算法在未注册的图表数据集中运行,其中的节点可能不同。我们的方法自然延伸至标注的图表,并由一个新颖的上层框完成,可以用作嵌入空间格罗莫夫·瓦西斯坦的快速近似值。我们提供了数字证据,表明我们的方法对不超超超嵌入图形数据集以及在线图形子空间估计和跟踪的兴趣。