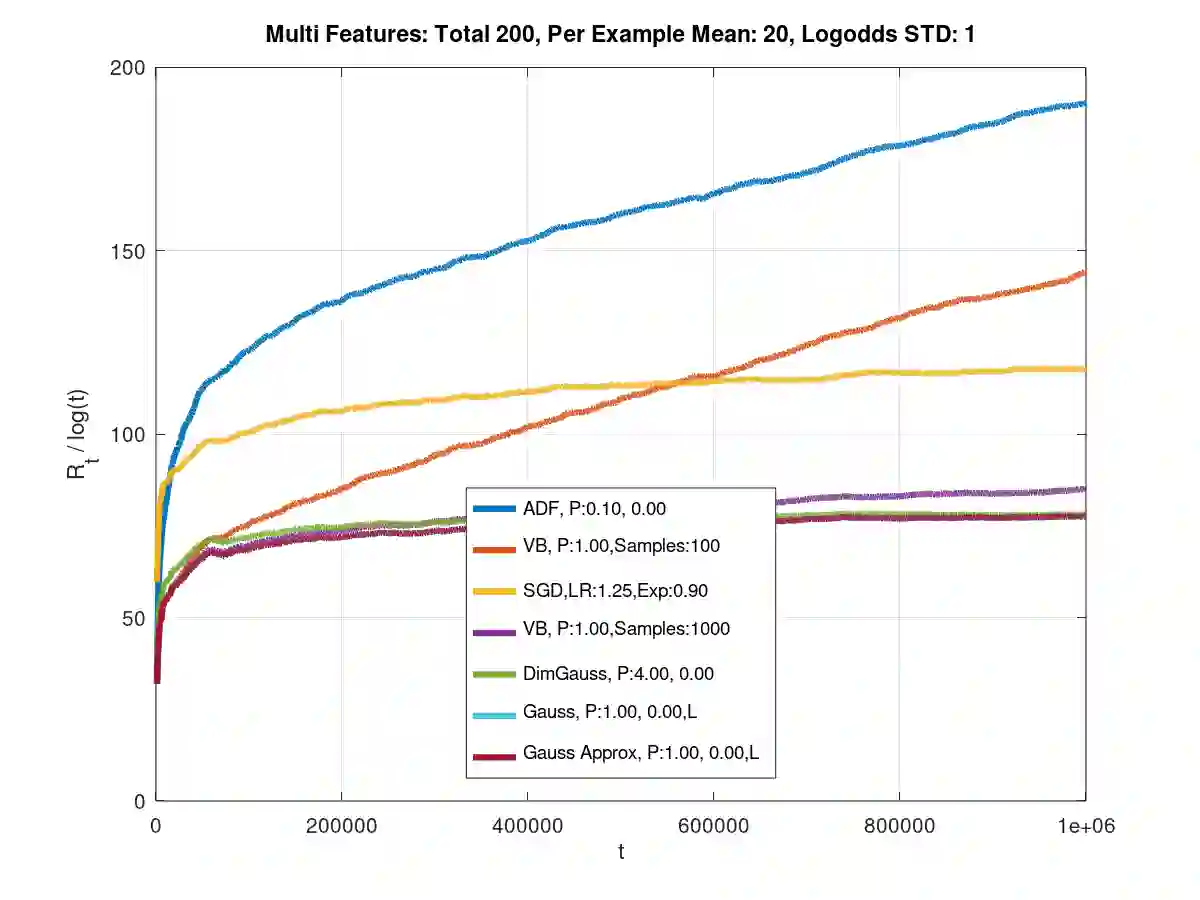
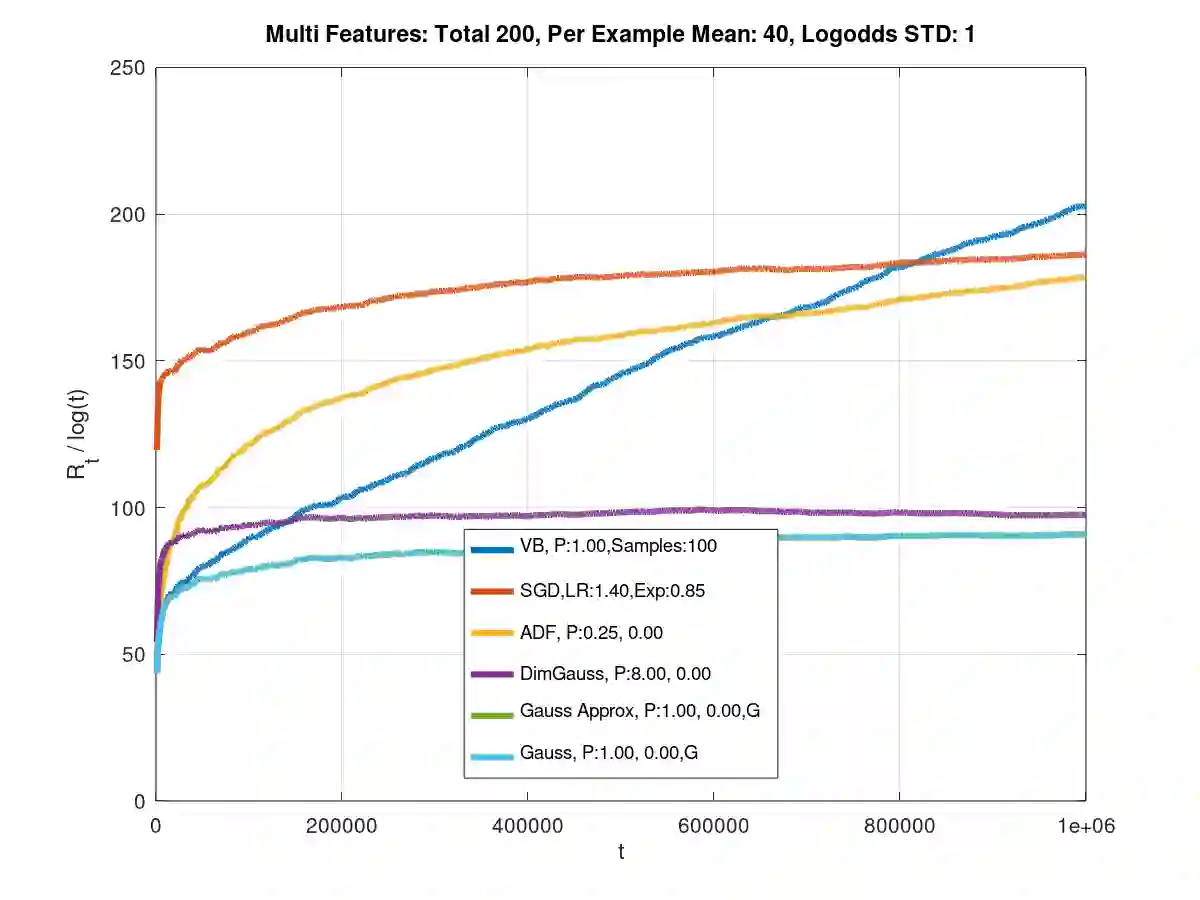
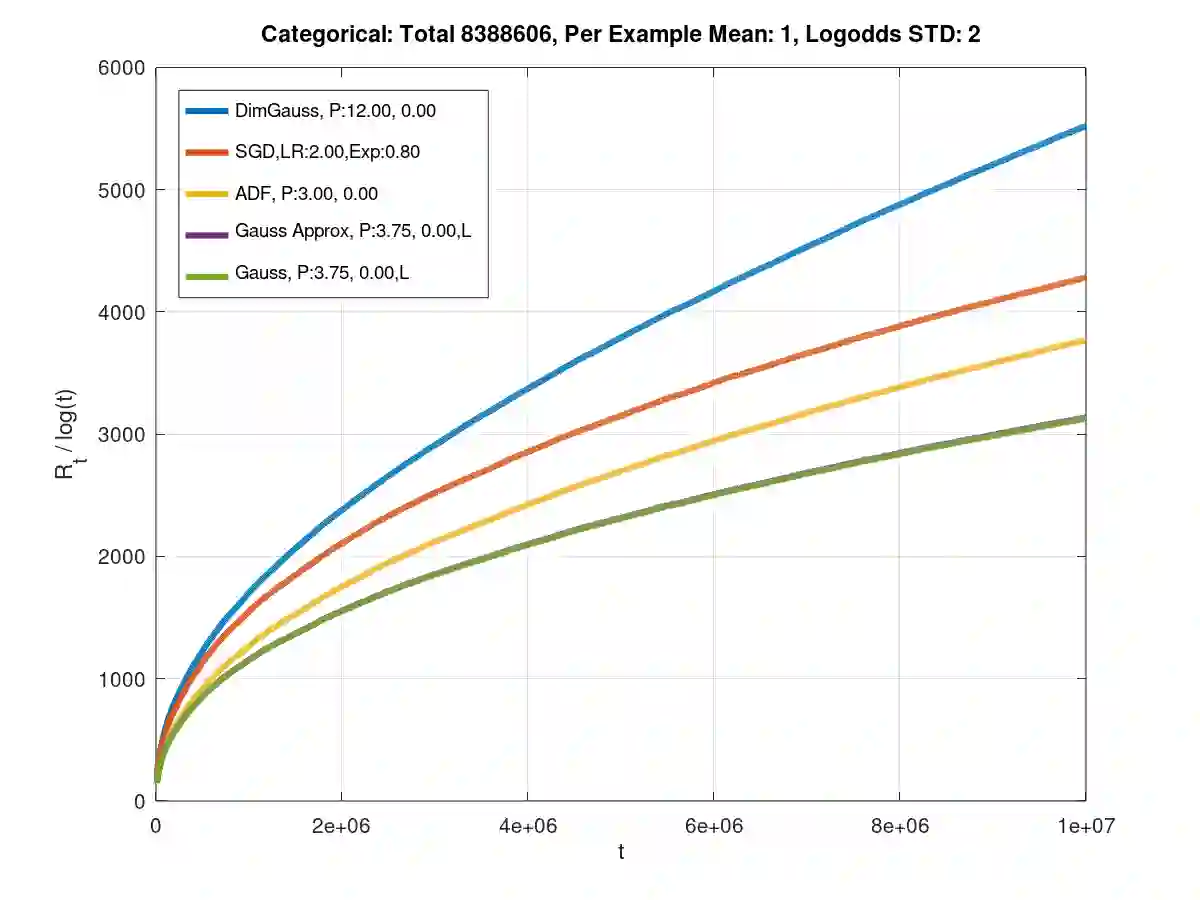
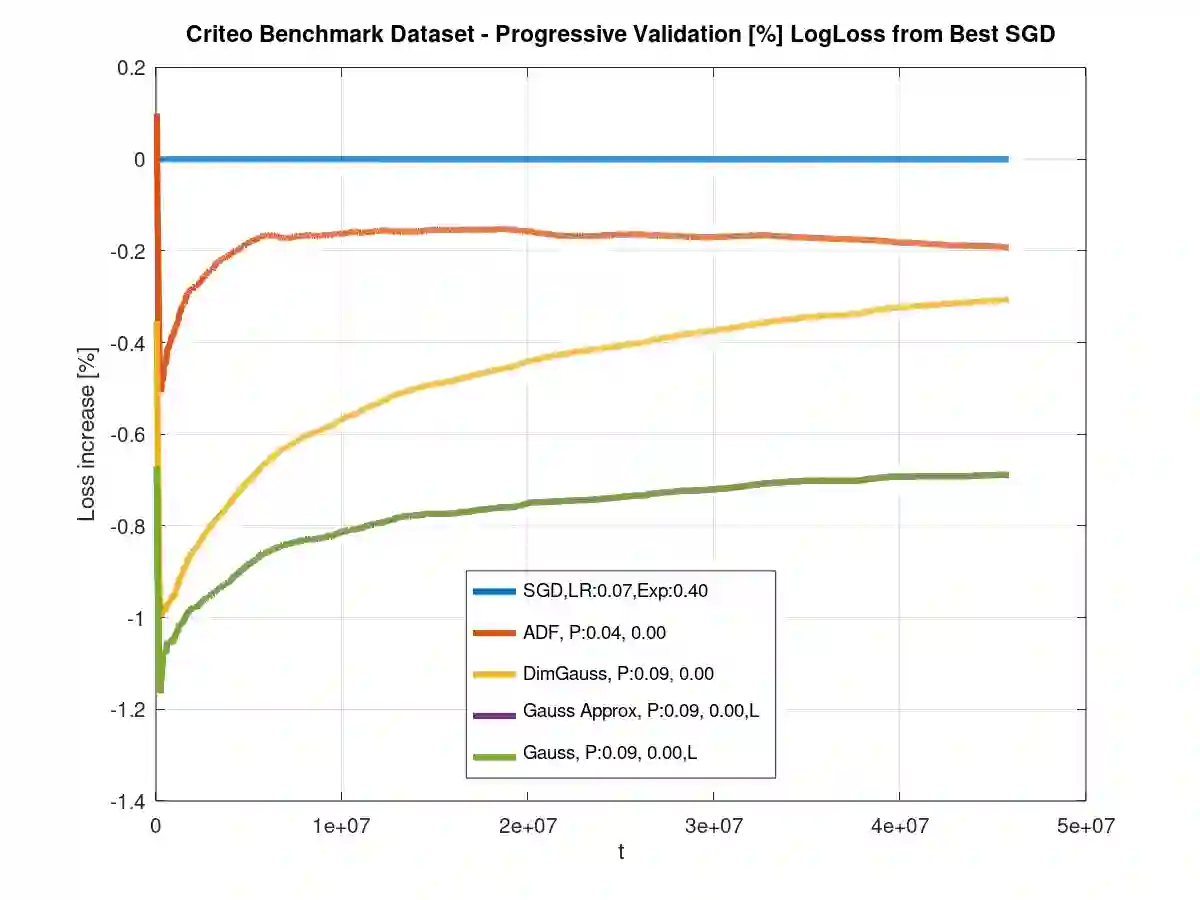
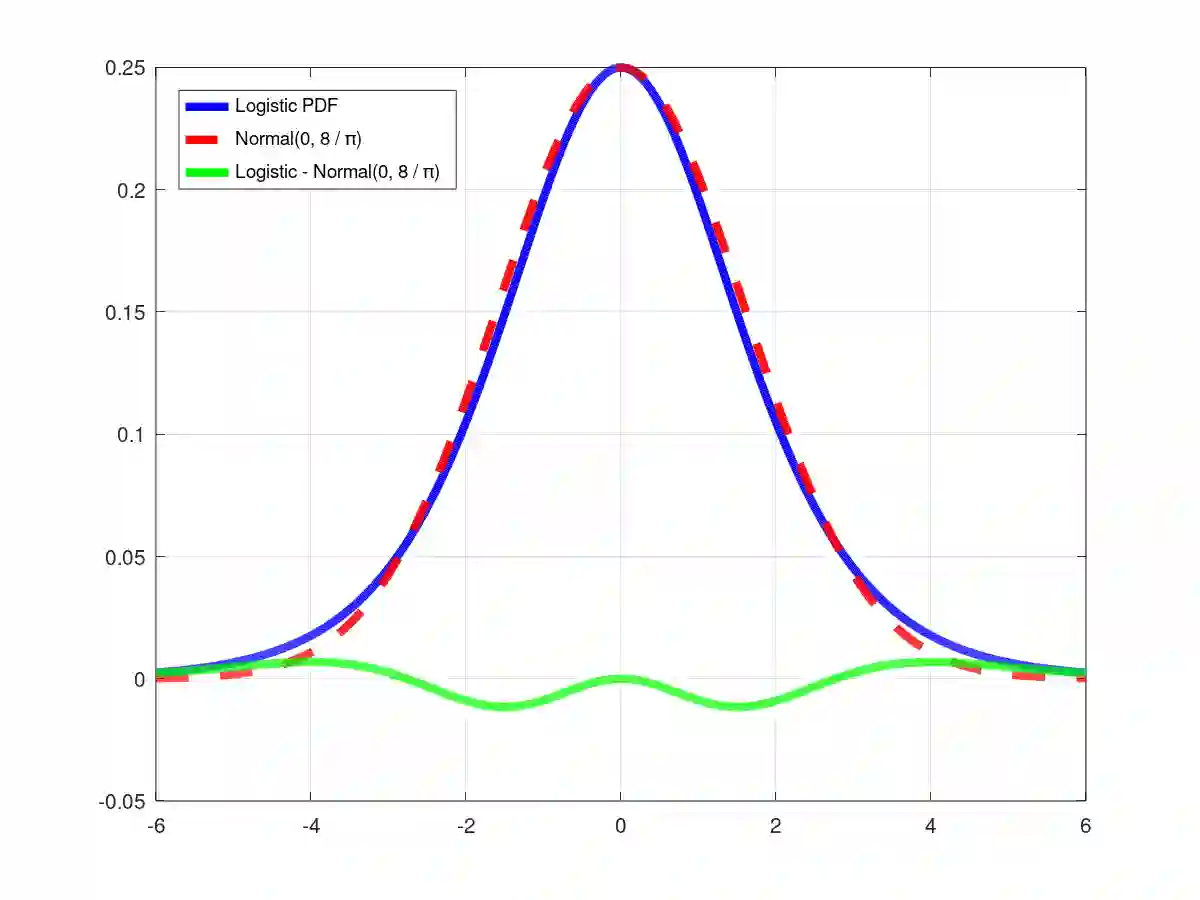
Theoretical results show that Bayesian methods can achieve lower bounds on regret for online logistic regression. In practice, however, such techniques may not be feasible especially for very large feature sets. Various approximations that, for huge sparse feature sets, diminish the theoretical advantages, must be used. Often, they apply stochastic gradient methods with hyper-parameters that must be tuned on some surrogate loss, defeating theoretical advantages of Bayesian methods. The surrogate loss, defined to approximate the mixture, requires techniques as Monte Carlo sampling, increasing computations per example. We propose low complexity analytical approximations for sparse online logistic and probit regressions. Unlike variational inference and other methods, our methods use analytical closed forms, substantially lowering computations. Unlike dense solutions, as Gaussian Mixtures, our methods allow for sparse problems with huge feature sets without increasing complexity. With the analytical closed forms, there is also no need for applying stochastic gradient methods on surrogate losses, and for tuning and balancing learning and regularization hyper-parameters. Empirical results top the performance of the more computationally involved methods. Like such methods, our methods still reveal per feature and per example uncertainty measures.
翻译:理论结果表明,贝叶斯方法可以降低对在线物流回归的遗憾程度。然而,在实践中,这种技术可能不可行,特别是对于非常大的功能组。对于极为稀少的功能组,必须使用各种近似方法,对于极为稀少的功能组,这些近似方法会减少理论优势。通常,这些近似方法会采用高偏差梯度方法,对于某些代谢损失必须加以调整,从而挫败了巴伊西亚方法的理论优势。代孕损失的定义是接近混合物,因此需要采用蒙特卡洛取样技术,增加每个例子的计算。我们建议对稀少的在线物流和标本回归采用低复杂性分析近似值。与变异性推断和其他方法不同,我们的方法使用分析封闭的形式,大大降低计算。与密集的解决方案不同,如高比斯混集体,我们的方法允许在不增加复杂性的情况下处理巨大特征组的稀疏问题。由于分析封闭形式,也没有必要对代孕变梯度方法加以应用,以及调整和平衡超度计的学习和调整。与差异分析方法不同的是,我们更精确性方法的顶级结果。