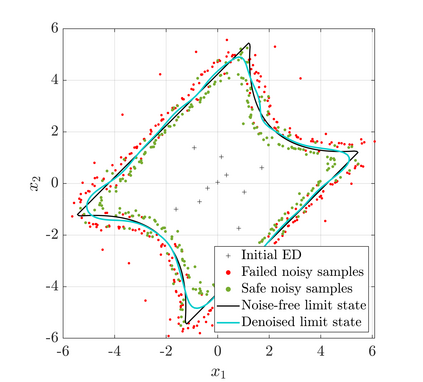
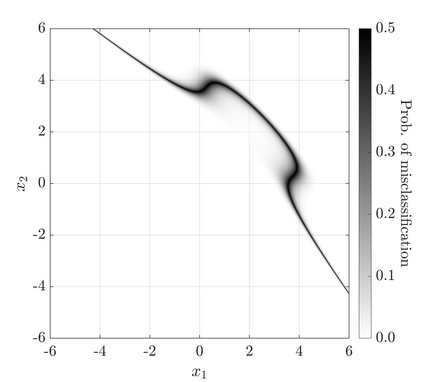
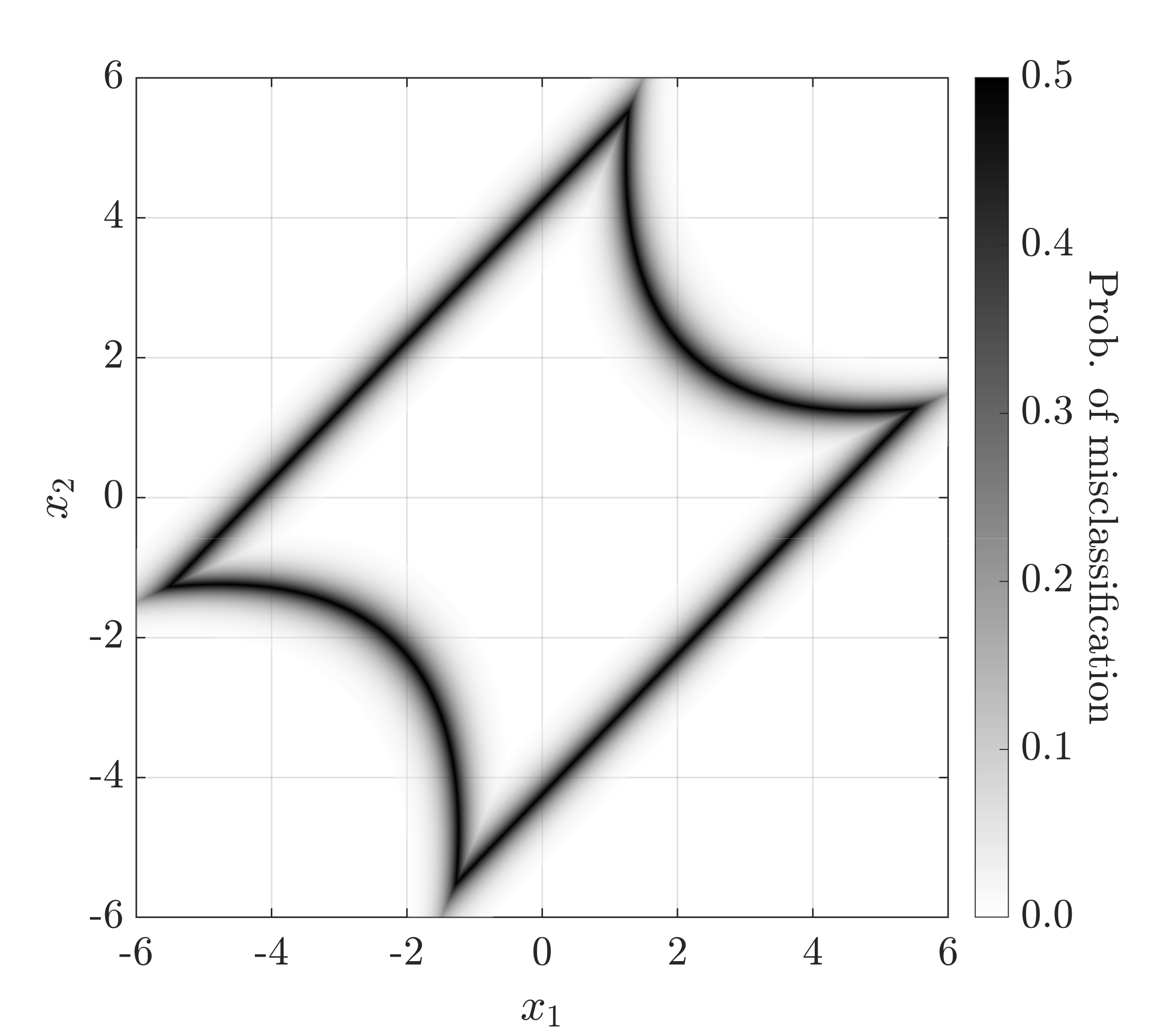
Reliability analysis for data-driven noisy models using active learning

Reliability analysis aims at estimating the failure probability of an engineering system. It often requires multiple runs of a limit-state function, which usually relies on computationally intensive simulations. Traditionally, these simulations have been considered deterministic, i.e., running them multiple times for a given set of input parameters always produces the same output. However, this assumption does not always hold, as many studies in the literature report non-deterministic computational simulations (also known as noisy models). In such cases, running the simulations multiple times with the same input will result in different outputs. Similarly, data-driven models that rely on real-world data may also be affected by noise. This characteristic poses a challenge when performing reliability analysis, as many classical methods, such as FORM and SORM, are tailored to deterministic models. To bridge this gap, this paper provides a novel methodology to perform reliability analysis on models contaminated by noise. In such cases, noise introduces latent uncertainty into the reliability estimator, leading to an incorrect estimation of the real underlying reliability index, even when using Monte Carlo simulation. To overcome this challenge, we propose the use of denoising regression-based surrogate models within an active learning reliability analysis framework. Specifically, we combine Gaussian process regression with a noise-aware learning function to efficiently estimate the probability of failure of the underlying noise-free model. We showcase the effectiveness of this methodology on standard benchmark functions and a finite element model of a realistic structural frame.