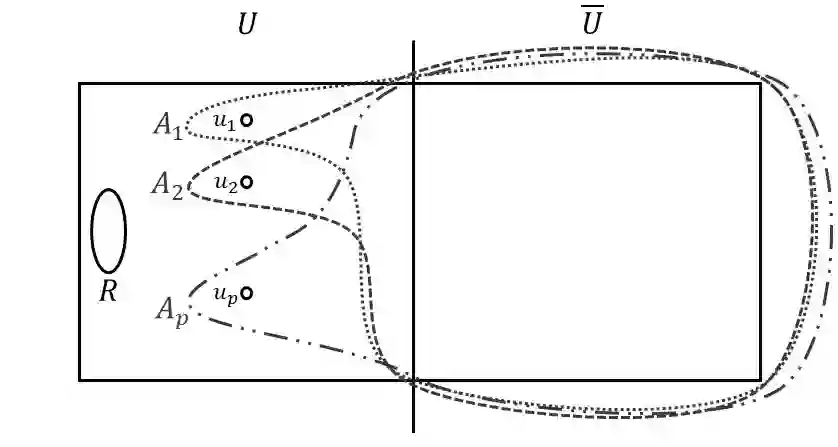
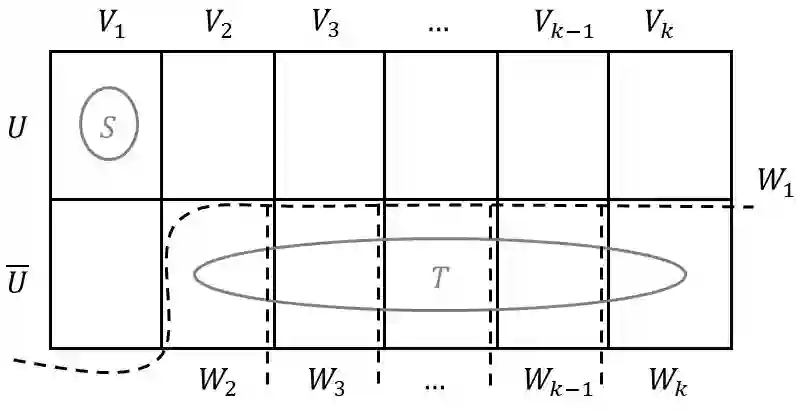
We consider the problem of deterministically enumerating all minimum $k$-cut-sets in a given hypergraph for any fixed $k$. The input here is a hypergraph $G = (V, E)$ with non-negative hyperedge costs. A subset $F$ of hyperedges is a $k$-cut-set if the number of connected components in $G - F$ is at least $k$ and it is a minimum $k$-cut-set if it has the least cost among all $k$-cut-sets. For fixed $k$, we call the problem of finding a minimum $k$-cut-set as Hypergraph-$k$-Cut and the problem of enumerating all minimum $k$-cut-sets as Enum-Hypergraph-$k$-Cut. The special cases of Hypergraph-$k$-Cut and Enum-Hypergraph-$k$-Cut restricted to graph inputs are well-known to be solvable in (randomized as well as deterministic) polynomial time. In contrast, it is only recently that polynomial-time algorithms for Hypergraph-$k$-Cut were developed. The randomized polynomial-time algorithm for Hypergraph-$k$-Cut that was designed in 2018 (Chandrasekaran, Xu, and Yu, SODA 2018) showed that the number of minimum $k$-cut-sets in a hypergraph is $O(n^{2k-2})$, where $n$ is the number of vertices in the input hypergraph, and that they can all be enumerated in randomized polynomial time, thus resolving Enum-Hypergraph-$k$-Cut in randomized polynomial time. A deterministic polynomial-time algorithm for Hypergraph-$k$-Cut was subsequently designed in 2020 (Chandrasekaran and Chekuri, FOCS 2020), but it is not guaranteed to enumerate all minimum $k$-cut-sets. In this work, we give the first deterministic polynomial-time algorithm to solve Enum-Hypergraph-$k$-Cut (this is non-trivial even for $k = 2$). Our algorithms are based on new structural results that allow for efficient recovery of all minimum $k$-cut-sets by solving minimum $(S,T)$-terminal cuts. Our techniques give new structural insights even for enumerating all minimum cut-sets (i.e., minimum 2-cut-sets) in a given hypergraph.
翻译:我们考虑的是,在特定高压中,任何固定的美元(美元)美元(美元)美元(美元)美元(美元)美元(美元)美元(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元(美元)(美元(美元)(美元)(美元(美元)(美元)(美元)(美元(美元)(美元)(美元)(美元(美元)(美元)(美元(美元)(美元(美元)(美元)(美元(美元)(美元(美元)(美元)(美元(美元)(美元)(美元)(美元(美元)(美元(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元(美元)(美元(美元(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)(美元)