Efficient numerical valuation of European options under the two-asset Kou jump-diffusion model

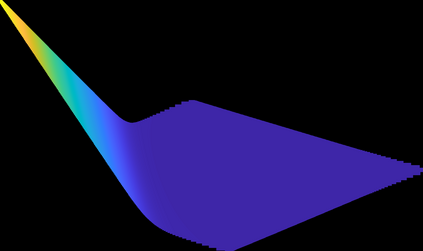
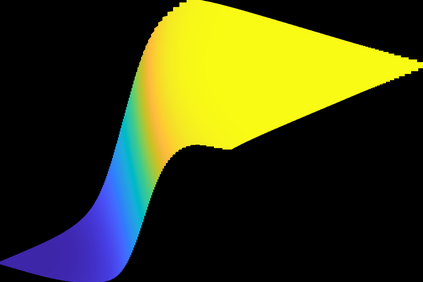
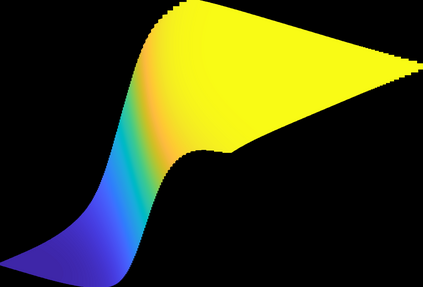
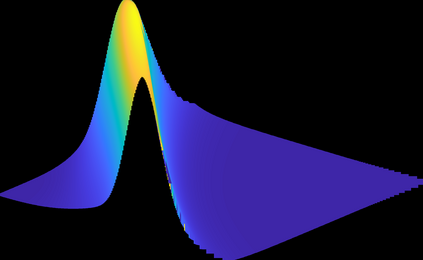
This paper concerns the numerical solution of the two-dimensional time-dependent partial integro-differential equation (PIDE) that holds for the values of European-style options under the two-asset Kou jump-diffusion model. A main feature of this equation is the presence of a nonlocal double integral term. For its numerical evaluation, we extend a highly efficient algorithm derived by Toivanen (2008) in the case of the one-dimensional Kou integral. The acquired algorithm for the two-dimensional Kou integral has optimal computational cost: the number of basic arithmetic operations is directly proportional to the number of spatial grid points in the semidiscretization. For the effective discretization in time, we study seven contemporary operator splitting schemes of the implicit-explicit (IMEX) and the alternating direction implicit (ADI) kind. All these schemes allow for a convenient, explicit treatment of the integral term. By ample numerical experiments for put-on-the-average option values, the stability and convergence behaviour as well as the mutual performance of the seven operator splitting schemes are investigated. Moreover, the Greeks Delta and Gamma are considered.