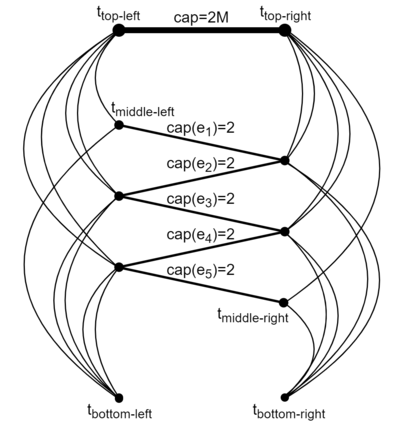
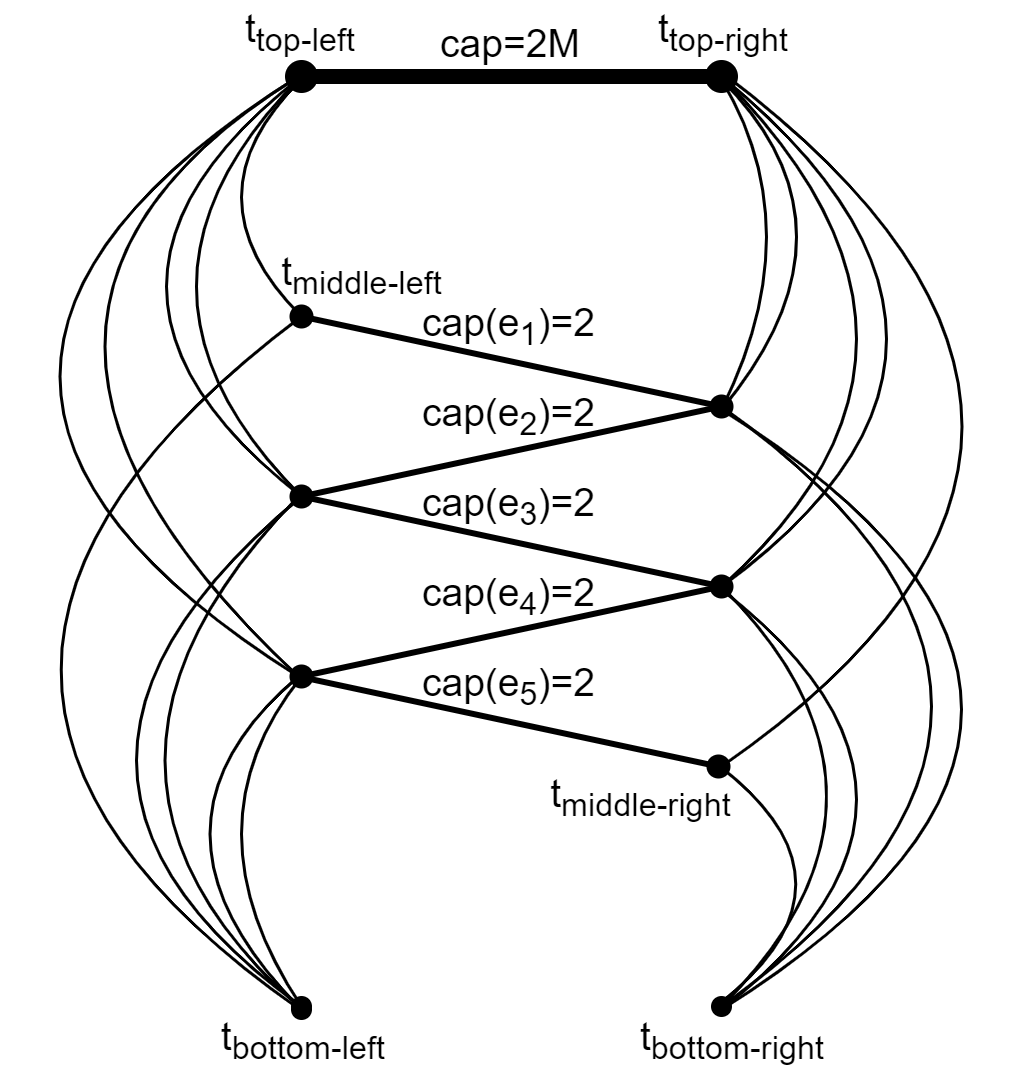
Given a large edge-capacitated network $G$ and a subset of $k$ vertices called terminals, an (exact) flow sparsifier is a small network $G'$ that preserves (exactly) all multicommodity flows that can be routed between the terminals. Flow sparsifiers were introduced by Leighton and Moitra [STOC 2010], and have been studied and used in many algorithmic contexts. A fundamental question that remained open for over a decade, asks whether every $k$-terminal network admits an exact flow sparsifier whose size is bounded by some function $f(k)$ (regardless of the size of $G$ or its capacities). We resolve this question in the negative by proving that there exist $6$-terminal networks $G$ whose flow sparsifiers $G'$ must have arbitrarily large size. This unboundedness is perhaps surprising, since the analogous sparsification that preserves all terminal cuts (called exact cut sparsifier or mimicking network) admits sparsifiers of size $f_0(k)\leq 2^{2^k}$ [Hagerup, Katajainen, Nishimura, and Ragde, JCSS 1998]. We prove our results by analyzing the set of all feasible demands in the network, known as the demand polytope. We identify an invariant of this polytope, essentially the slope of certain facets, that can be made arbitrarily large even for $k=6$, and implies an explicit lower bound on the size of the network. We further use this technique to answer, again in the negative, an open question of Seymour [JCTB 2015] regarding flow-sparsification that uses only contractions and preserves the infeasibility of one demand vector.
翻译:鉴于一个巨大的边缘能力网络$G$和一个叫做“终端”的子节基脊椎,一个(精准的)流动封闭器是一个小网络$G$,它保存了(精确的)所有可在终端之间选择的多通流流(精确的)所有多通性流流流。流动封闭器由Leighton和Moitra[STOC 2010]推出,并在许多算法背景下被研究和使用。一个持续了十多年的根本性问题,问每个美元终点网络是否都承认一个精确的流量过滤器,其大小基本上受某种功能$(k)的流量(k),是一个小的网络$G$(具体地),它保存了所有开放性断层(称为“精确的缩压器”或“缩压”网络的精确化器。我们用这个已知的基流流、Sain=eqnal的系统,它再次使用。