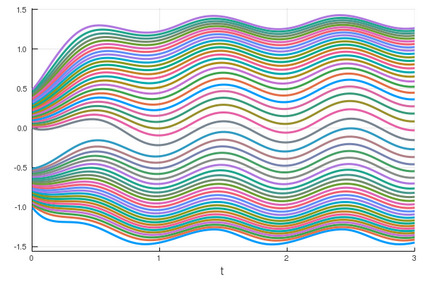
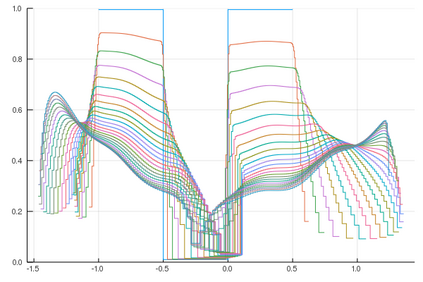
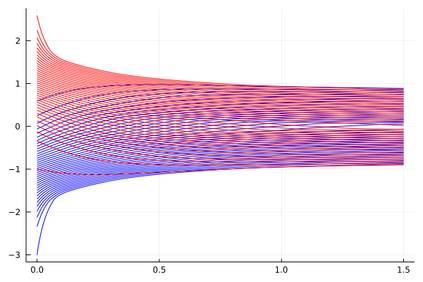
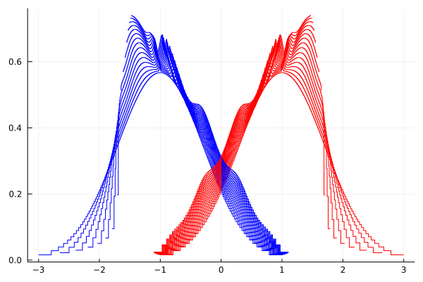
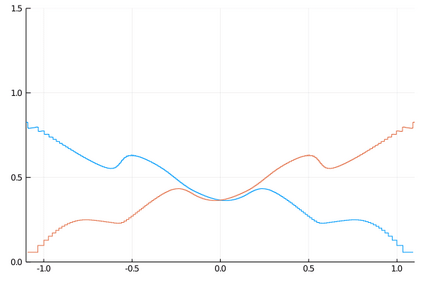
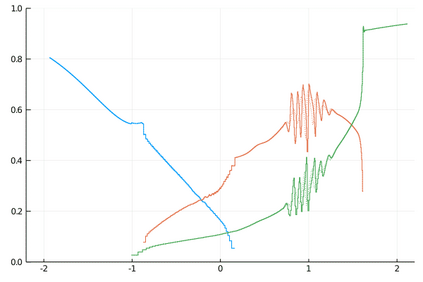
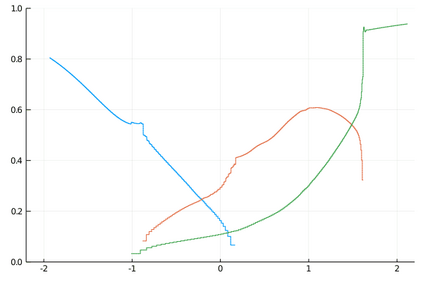
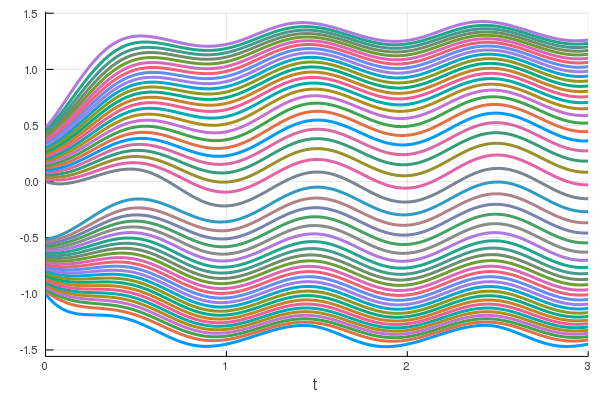
We develop deterministic particle schemes to solve non-local scalar conservation laws with congestion. We show that the discrete approximations converge to the unique entropy solution with an explicit rate of convergence under more general assumptions that the existing literature: the velocity fields are less regular (in particular the interaction force can have a discontinuity at the origin) with no prescribed attractive/repulsive regime and the mobility can have unbounded support. We complement our results with some numerical simulations, among which we show the applicability of the schemes to the multi-species setting.
翻译：我们制定了确定性的粒子计划,以解决非本地的天秤保护法的拥挤问题。我们表明,离散近似值与独有的酶溶液相汇合,在更笼统的假设下有明确的趋同率,即现有文献:速度场不太固定(特别是互动力在来源地可能不连续),没有规定的有吸引力/有弹性的制度,流动性可以不受限制地提供支持。我们用一些数字模拟来补充我们的结果,其中我们展示了这些办法对多物种环境的适用性。
相关内容
微信扫码咨询专知VIP会员