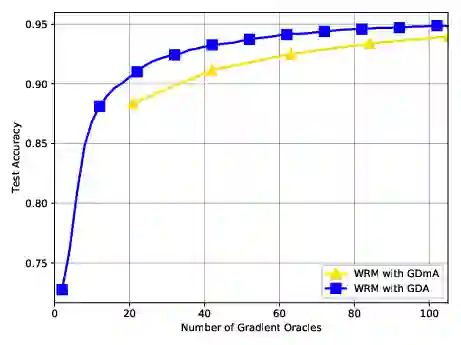
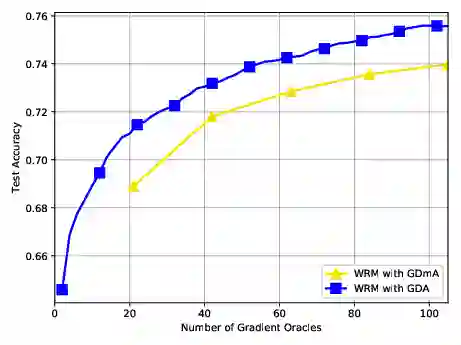
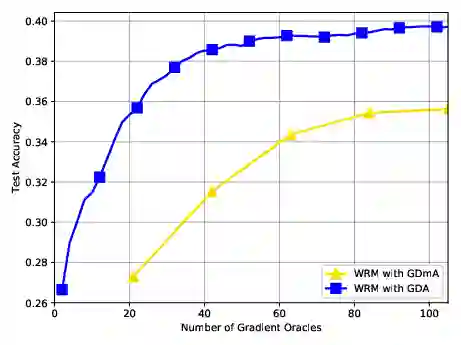
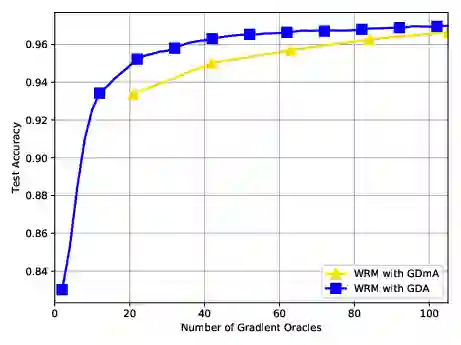
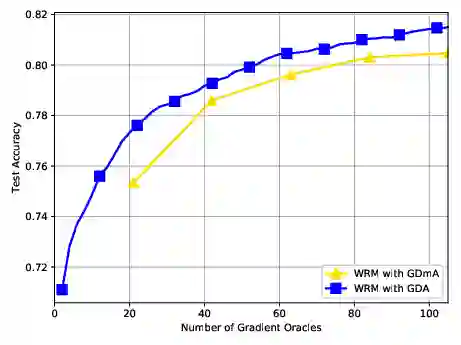
We consider nonconvex-concave minimax problems, $\min_{\mathbf{x}} \max_{\mathbf{y} \in \mathcal{Y}} f(\mathbf{x}, \mathbf{y})$, where $f$ is nonconvex in $\mathbf{x}$ but concave in $\mathbf{y}$ and $\mathcal{Y}$ is a convex and bounded set. One of the most popular algorithms for solving this problem is the celebrated gradient descent ascent (GDA) algorithm, which has been widely used in machine learning, control theory and economics. Despite the extensive convergence results for the convex-concave setting, GDA with equal stepsize can converge to limit cycles or even diverge in a general setting. In this paper, we present the complexity results on two-time-scale GDA for solving nonconvex-concave minimax problems, showing that the algorithm can find a stationary point of the function $\Phi(\cdot) := \max_{\mathbf{y} \in \mathcal{Y}} f(\cdot, \mathbf{y})$ efficiently. To the best our knowledge, this is the first nonasymptotic analysis for two-time-scale GDA in this setting, shedding light on its superior practical performance in training generative adversarial networks (GANs) and other real applications.
翻译:我们考虑的是非convex- concave minimax 问题, $\ min{ mathbf{ { mathbf{x{ { max{ { max{ maxbf{ y}} $\ mathcal{ { mathbf{x} $, 美元是非confx} 和 $\ mathcal{ Y} 美元, 是一个螺旋和捆绑的套件。 解决这一问题最流行的非流行算法之一是在机器学习、 控制理论和经济中广泛使用的 mothcal descal{Y\\ frb{ fr} 运算法。 尽管对 convex concave 设置有广泛的趋同结果, 但具有等阶的 GDADA可以组合到限制周期, 甚至在一般设置中。 本文中, 我们展示了用于解决非convex minix 缩缩算的两次的 GDAA 的复杂结果。 显示, 此算算算算法可以找到 $x max fisax= fal= freal= fix fix fix freal
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem