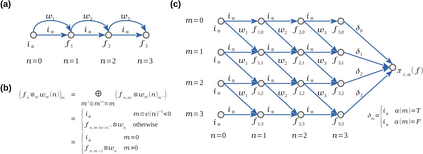
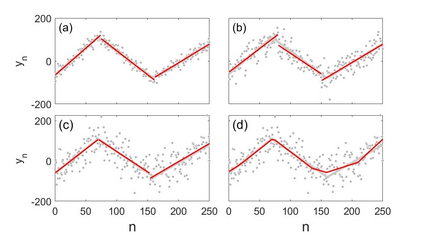
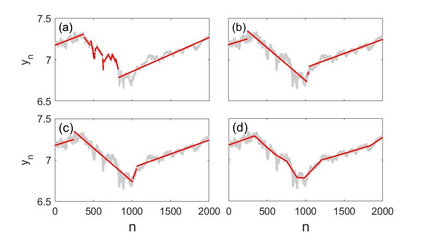
Dynamic programming (DP) is a broadly applicable algorithmic design paradigm for the efficient, exact solution of otherwise intractable, combinatorial problems. However, the design of such algorithms is often presented informally in an ad-hoc manner, and as a result is often difficult to apply correctly. In this paper, we present a rigorous algebraic formalism for systematically deriving novel DP algorithms, either from existing DP algorithms or from simple functional recurrences. These derivations lead to algorithms which are provably correct and polymorphic over any semiring, which means that they can be applied to the full scope of combinatorial problems expressible in terms of semirings. This includes, for example: optimization, optimal probability and Viterbi decoding, probabilistic marginalization, logical inference, fuzzy sets, differentiable softmax, and relational and provenance queries. The approach, building on many ideas from the existing literature on constructive algorithmics, exploits generic properties of (semiring) polymorphic functions, tupling and formal sums (lifting), and algebraic simplifications arising from constraint algebras. We demonstrate the effectiveness of this formalism for some example applications arising in signal processing, bioinformatics and reliability engineering.
翻译:动态编程(DP)是一个广泛应用的算法设计范例,用于有效、精确地解决其他棘手的组合问题。然而,这种算法的设计往往以临时方式非正式地提出,因此往往难以正确应用。在本文中,我们提出了一种严格的代数形式主义,以便系统地从现有的DP算法或简单的功能重现中得出新的DP算法。这些衍生法导致算法,这种算法可以被确认为正确和多变,而任何半成型都意味着这些算法可以适用于从半成型中可以看出的组合问题的全部范围。例如:优化、最佳概率和维泰比解码、概率边缘化、逻辑推论、模糊性套件、不同的软体缩、关系和证明性查询。这种方法借鉴了现有文献中关于建设性算法的许多想法,利用了(扩大的)多变形功能的通用特性、调制和正式调制(提振),以及从生物工程的正规化和信号处理中产生的某些变压性简化性应用。