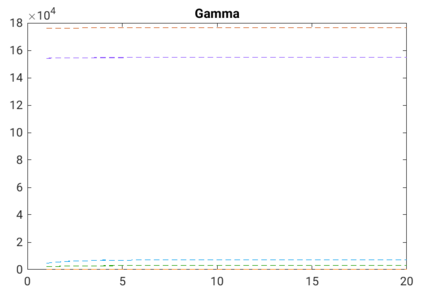
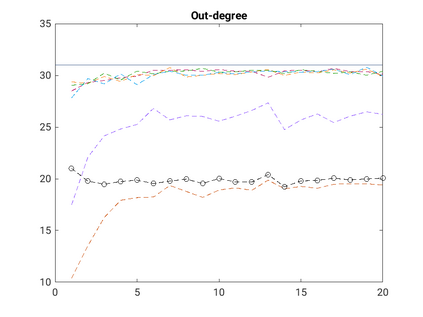
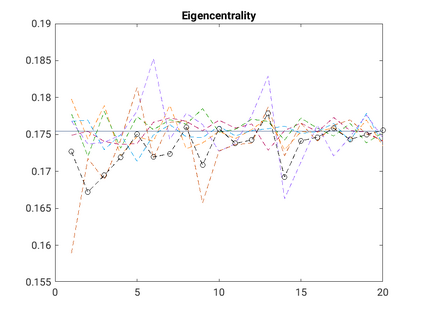
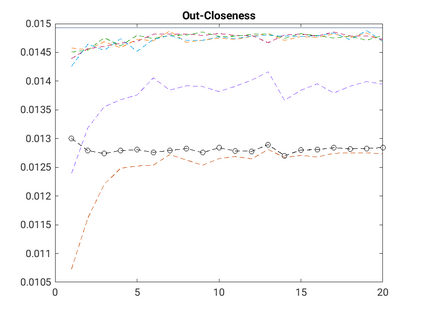
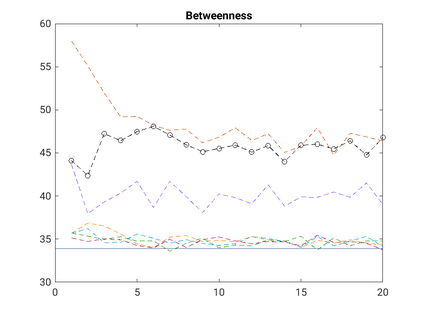
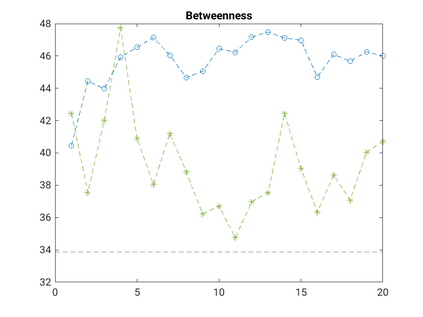
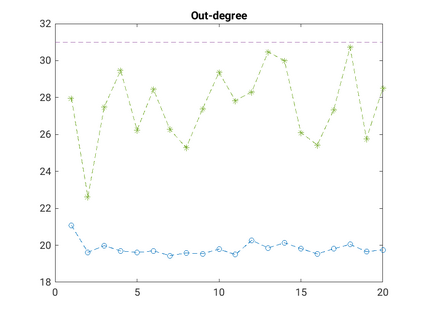
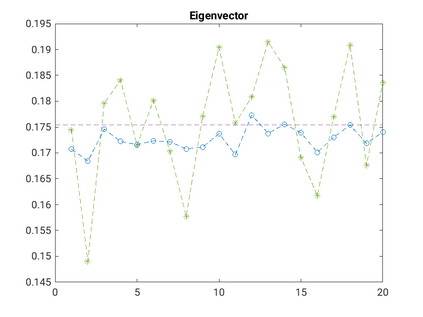
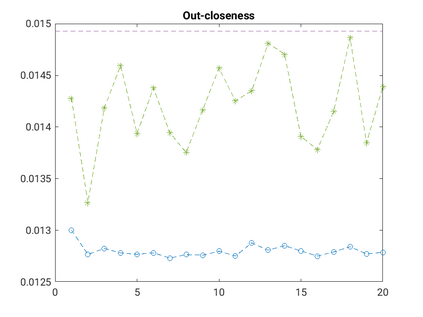
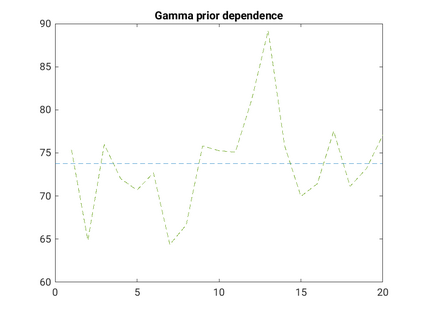
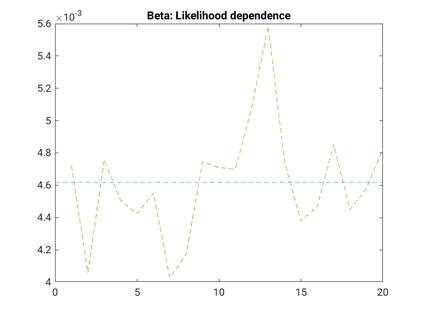
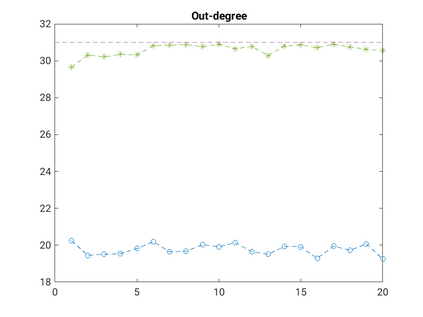
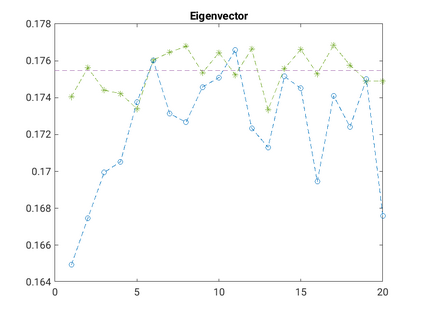
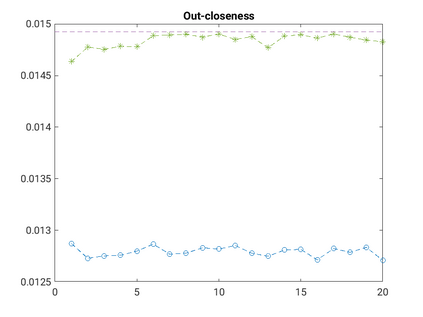
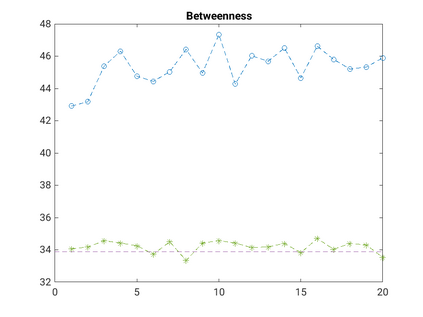
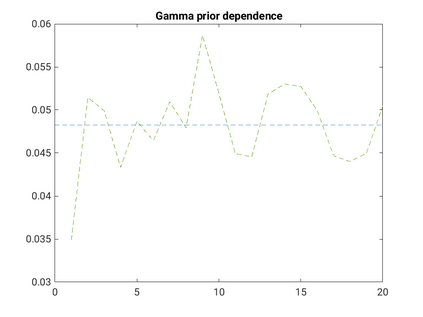
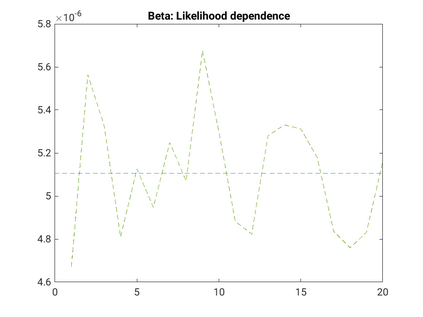
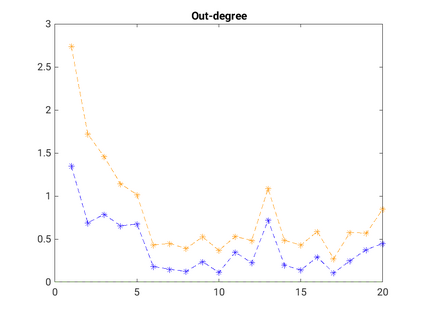
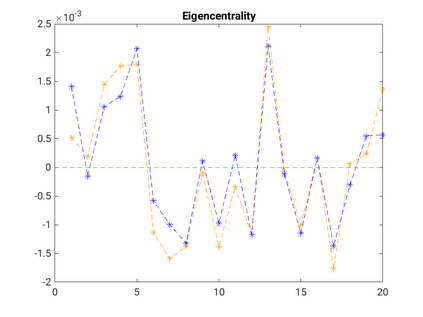
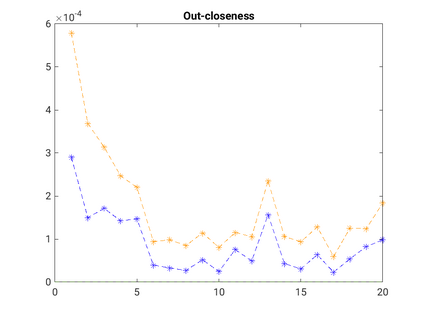
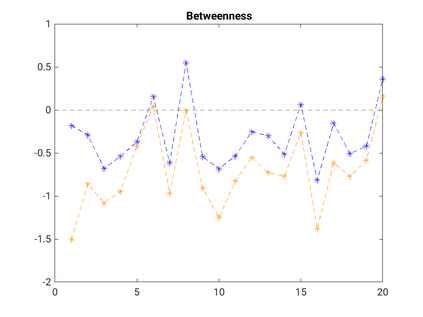
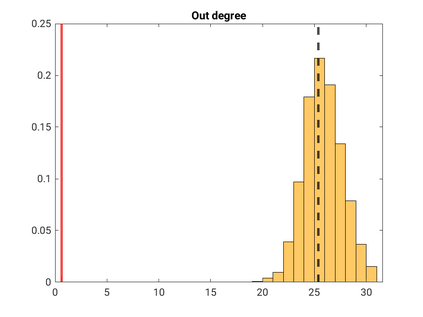
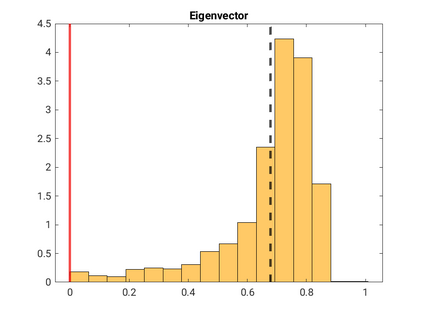
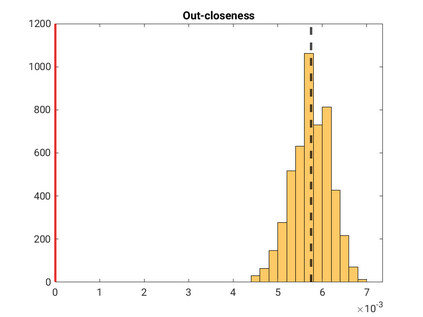
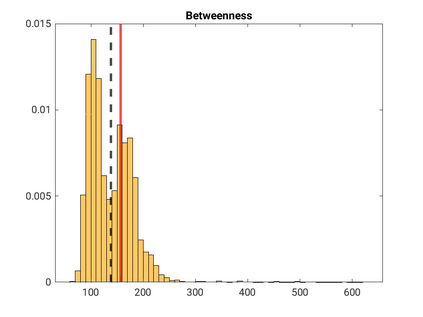
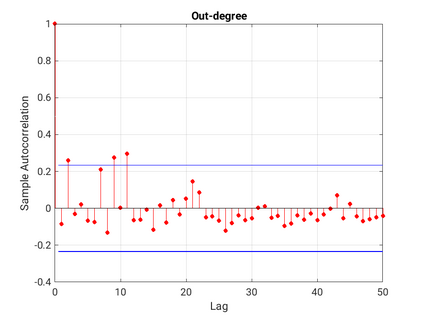
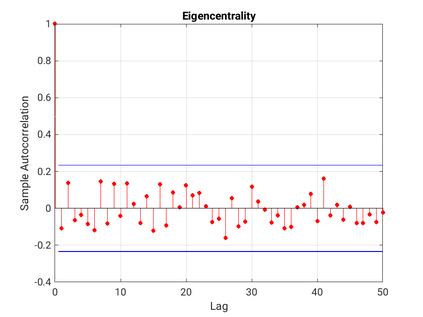
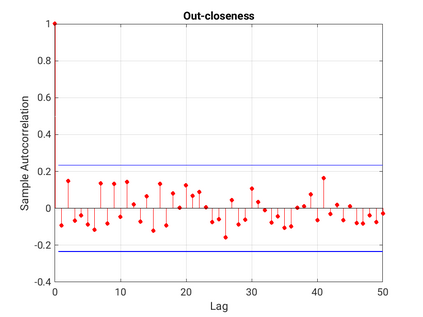
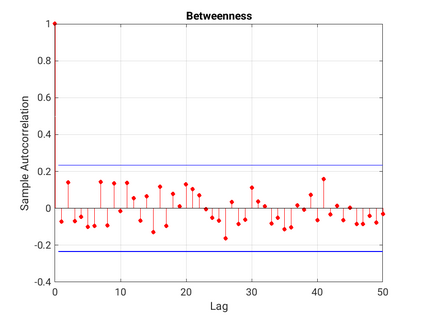
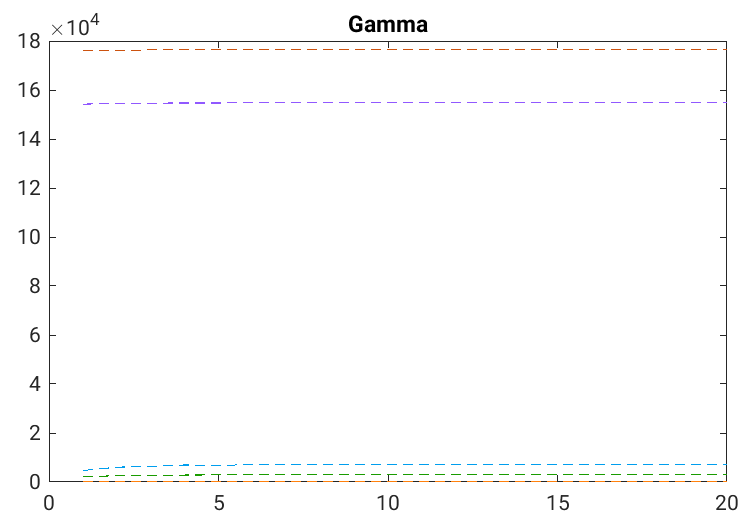
Modelling noisy data in a network context remains an unavoidable obstacle; fortunately, random matrix theory may comprehensively describe network environments effectively. Thus it necessitates the probabilistic characterisation of these networks (and accompanying noisy data) using matrix variate models. Denoising network data using a Bayes approach is not common in surveyed literature. This paper adopts the Bayesian viewpoint and introduces a new matrix variate t-model in a prior sense by relying on the matrix variate gamma distribution for the noise process, following the Gaussian graphical network for the cases when the normality assumption is violated. From a statistical learning viewpoint, such a theoretical consideration indubitably benefits the real-world comprehension of structures causing noisy data with network-based attributes as part of machine learning in data science. A full structural learning procedure is provided for calculating and approximating the resulting posterior of interest to assess the considered model's network centrality measures. Experiments with synthetic and real-world stock price data are performed not only to validate the proposed algorithm's capabilities but also to show that this model has wider flexibility than originally implied in Billio et al. (2021).
翻译:暂无翻译