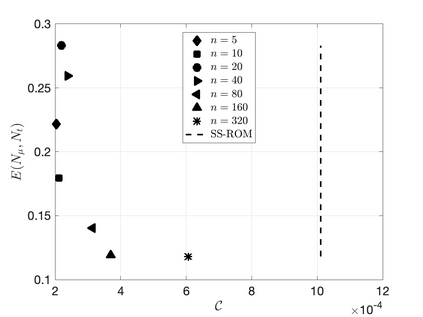
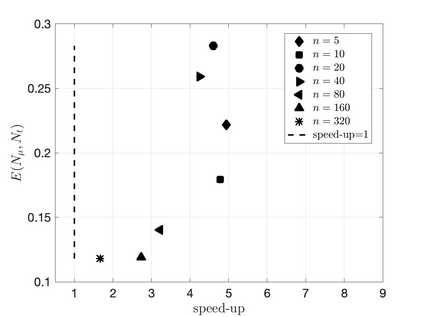
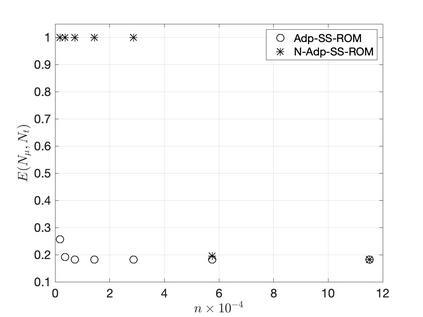
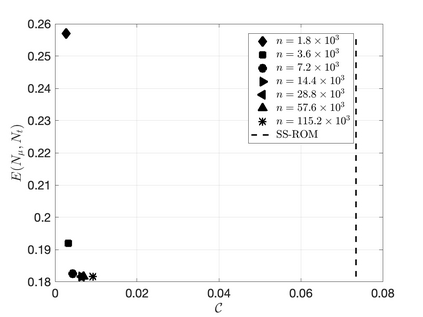
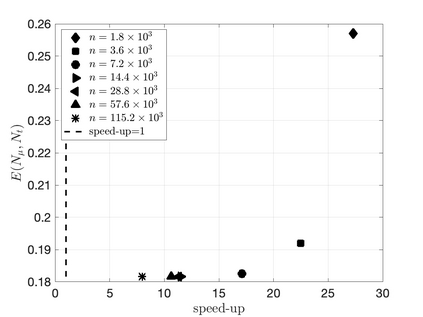
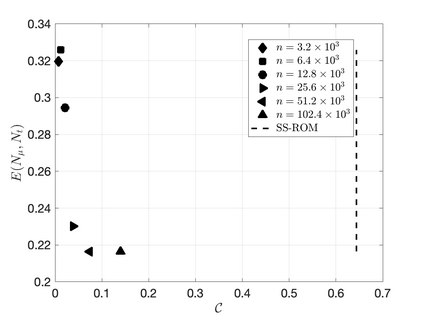
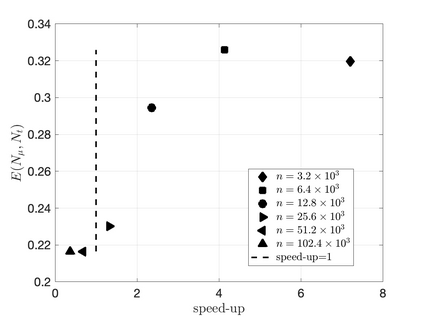
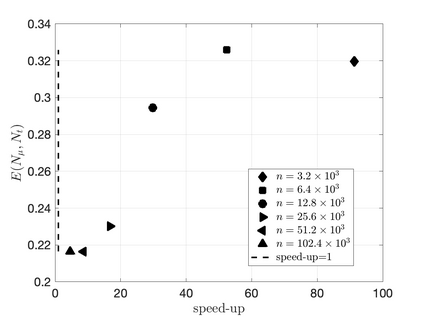
We propose an efficient residual minimization technique for the nonlinear model-order reduction of parameterized hyperbolic partial differential equations. Our nonlinear approximation space is a span of snapshots evaluated on a shifted spatial domain, and we compute our reduced approximation via residual minimization. To speed-up the residual minimization, we compute and minimize the residual on a (preferably small) subset of the mesh, the so-called reduced mesh. Due to the nonlinearity of our approximation space we show that, similar to the solution, the residual also exhibits transport-type behaviour. To account for this behaviour, we introduce online-adaptivity in the reduced mesh by "moving" it along the spatial domain with parameter dependent shifts. We also present an extension of our method to spatial transforms different from shifting. Numerical experiments showcase the effectiveness of our method and the inaccuracies resulting from a non-adaptive reduced mesh.
翻译:我们为参数化双曲部分偏差方程式的非线性模型级削减提出了高效的剩余最小化技术。 我们的非线性近似空间空间是一个在移动空间域上评估的片段, 我们通过剩余最小化来计算我们减少的近近近。 为了加快剩余最小化的速度, 我们计算并最小化剩余部分在网格中一个( 最好是很小的) 子( 所谓的缩小网格 ) 。 由于我们近似空间的不线性, 我们显示, 与解决方案相似, 剩余部分也表现出了迁移类型的行为。 为了说明这种行为, 我们通过“ 移动” 将网状缩放到空间域的网状上, 并加上参数依赖的变化 。 我们还展示了我们的方法与移动不同的空间变异的延伸方法。 数字实验展示了我们的方法的有效性以及非适应性缩小网格所产生的不准确性。