Non-asymptotic confidence bands on the probability an individual benefits from treatment (PIBT)

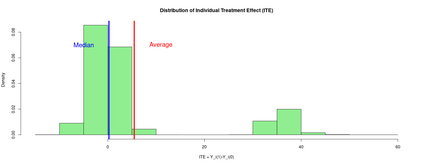
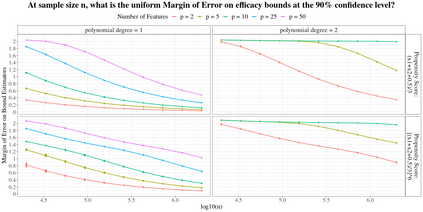
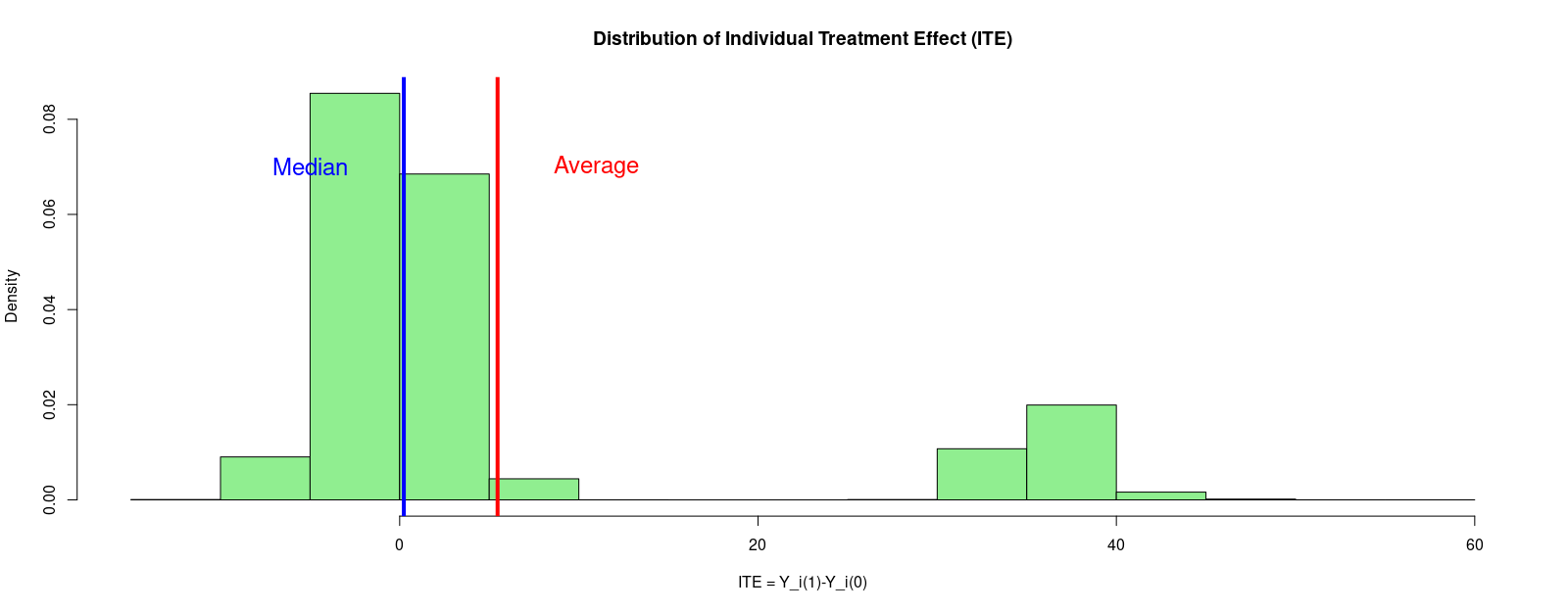
The premise of this work, in a vein similar to predictive inference with quantile regression, is that observations may lie far away from their conditional expectation. In the context of causal inference, due to the missing-ness of one outcome, it is difficult to check whether an individual's treatment effect lies close to its prediction given by the estimated Average Treatment Effect (ATE) or Conditional Average Treatment Effect (CATE). With the aim of augmenting the inference with these estimands in practice, we further study an existing distribution-free framework for the plug-in estimation of bounds on the probability an individual benefits from treatment (PIBT), a generally inestimable quantity that would concisely summarize an intervention's efficacy if it could be known. Given the innate uncertainty in the target population-level bounds on PIBT, we seek to better understand the margin of error for the estimation of these target parameters in order to help discern whether estimated bounds on treatment efficacy are tight (or wide) due to random chance or not. In particular, we present non-asymptotic guarantees to the estimation of bounds on marginal PIBT for a randomized controlled trial (RCT) setting. We also derive new non-asymptotic results for the case where we would like to understand heterogeneity in PIBT across strata of pre-treatment covariates, with one of our main results in this setting making strategic use of regression residuals. These results, especially those in the RCT case, can be used to help with formal statistical power analyses and frequentist confidence statements for settings where we are interested in inferring PIBT through the target bounds under minimal parametric assumptions.