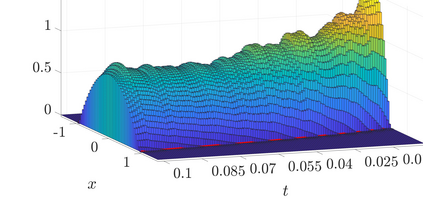
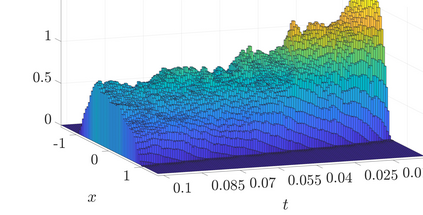
We study a general class of singular degenerate parabolic stochastic partial differential equations (SPDEs) which include, in particular, the stochastic porous medium equations and the stochastic fast diffusion equation. We propose a fully discrete numerical approximation of the considered SPDEs based on the very weak formulation. By exploiting the monotonicity properties of the proposed formulation we prove the convergence of the numerical approximation towards the unique solution. Furthermore, we construct an implementable finite element scheme for the spatial discretization of the very weak formulation and provide numerical simulations to demonstrate the practicability of the proposed discretization.
翻译:我们研究一个奇特的退化抛物线偏差部分偏差方程式(SPDEs)的一般类别,其中特别包括随机多孔介质方程式和随机多孔介质快速扩散方程式。我们建议根据非常弱的配方,对经过考虑的SPDEs提出完全独立的数字近似值。通过利用拟议配方的单音性特性,我们证明数字近似值与独特解决办法的趋同。此外,我们为非常弱的配方的空间离散构建了一个可执行的有限元素计划,并提供数字模拟,以证明提议的离散性是否可行。