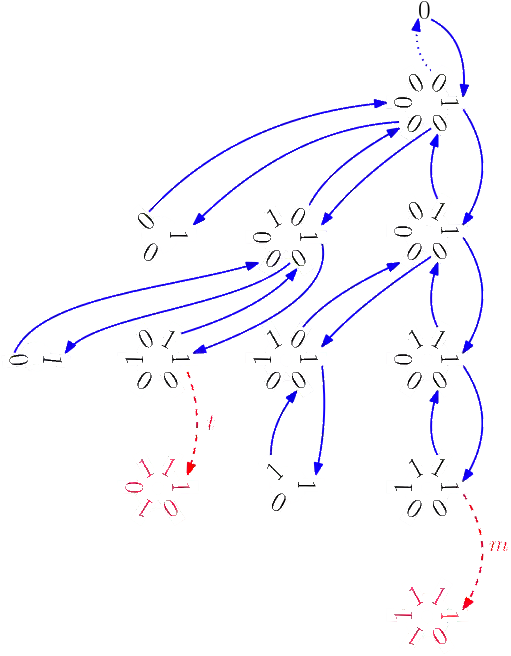
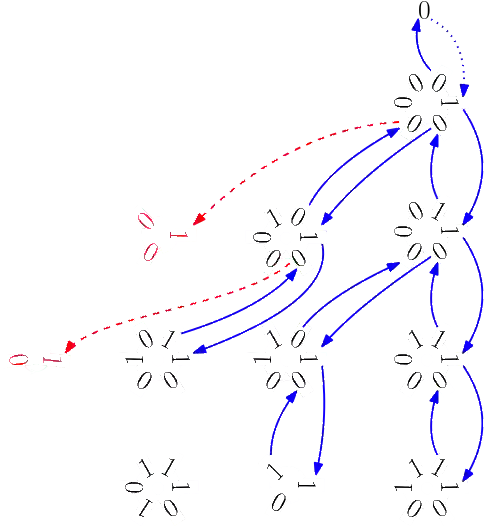
A cut-down de Bruijn sequence is a cyclic string of length $L$, where $1 \leq L \leq k^n$, such that every substring of length $n$ appears at most once. Etzion [Theor. Comp. Sci 44 (1986)] gives an algorithm to construct binary cut-down de Bruijn sequences that requires $o(n)$ simple $n$-bit operations per symbol generated. In this paper, we simplify the algorithm and improve the running time to $\mathcal{O}(n)$ time per symbol generated using $\mathcal{O}(n)$ space. We then provide the first successor-rule approach for constructing a binary cut-down de Bruijn sequence by leveraging recent ranking algorithms for fixed-density Lyndon words. Finally, we develop an algorithm to generate cut-down de Bruijn sequences for $k>2$ that runs in $\mathcal{O}(n)$ time per symbol using $\mathcal{O}(n)$ space after some initialization. While our $k$-ary algorithm is based on our simplified version of Etzion's binary algorithm, a number of non-trivial adaptations are required to generalize to larger alphabets.
翻译:布鲁伊恩断线序列是一个长长的周期字符串 $L$, 其中1\leq L\leq k ⁇ n$ 美元, 这样每个长度的子字符串最多出现一次 。 Etzion [Theor. comp. Sci 44 (1986) 提供一种算法, 用于构建布鲁伊恩的二进制切线序列, 每生成一个符号需要$(n) 简单美元比特操作。 在本文中, 我们简化算法, 并将运行时间改进到$\ mathcal{O} (n) 每个符号使用$\ mathcal{O} (n) 空间生成的时间。 我们然后提供第一个后续规则方法, 利用最近对固定密度 Lyndon 字的排序算法来构建一个二进制断线序列。 最后, 我们开发一个算法, 以美元比特2美元生成的断线操作。 以 $\ mathcal{O} (n) 每个符号使用$\mathcal{O} (n) (n) (n) ro) asubeption- rujallizalizalalalisalizalisalismacalisalisalisalislislation 。 。 需要将一个更小的硬化为普通化。