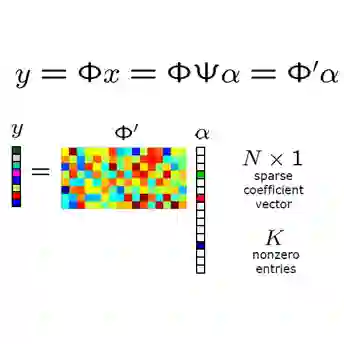
This paper explores the genotype-phenotype relationship. It outlines conditions under which the dependence of quantitative trait on the genome might be predictable, based on measurement of a limited subset of genotypes. It uses the theory of real-valued Boolean functions in a systematic way to translate trait data into the Fourier domain. Important trait features, such as the roughness of the trait landscape or the modularity of a trait have a simple Fourier interpretation. Roughness at a gene location corresponds to high sensitivity to mutation, while a modular organization of gene activity reduces such sensitivity. Traits where rugged loci are rare will naturally compress gene data in the Fourier domain, leading to a sparse representation of trait data, concentrated in identifiable, low-level coefficients. This Fourier representation of a trait organizes epistasis in a form which is isometric to the trait data. As Fourier matrices are known to be maximally incoherent with the standard basis, this permits employing compressive sensing techniques to work from data sets that are relatively small -- sometimes even polynomial -- compared to the exponentially large sets of possible genomes. This theory provides a theoretical underpinning for systematic use of Boolean function machinery to dissect the dependency of a trait on the genome and environment.
翻译:本文探讨了基因类型- pheno 类型关系。 它概述了基因组定量特征依赖性在哪些条件下可以预测, 其依据是对有限基因类型进行测量。 它以系统的方式使用实际价值的布尔函数理论, 将特质数据转换到 Fourier 域。 重要的特征特征, 如特质景观的粗糙度或特质的模块化具有简单的 Fourier 解释。 基因位置的粗糙相当于突变的高度敏感度, 而基因活动的模块化组织则降低了这种敏感度。 粗略的迷虫稀有的轨迹将自然压缩Fourier 域的基因数据,导致特征数据的稀薄表述, 集中在可识别的低水平系数中。 这种四倍的特质代表将特征组织成一种与特质数据不相匹配的形式。 众所周知, Fourier 基质与标准基础极为不相近, 这允许使用压缩的遥感技术从相对小的数据集( 有时甚至是多式) 进行工作, 与可能的大规模基因组群相比, 导致特性数据很少, 以可辨测为集中的特征数据。 这一理论理论将基因组用作基因组系系系的理论基础, 。