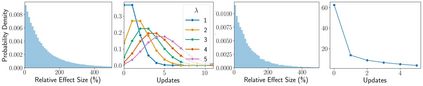
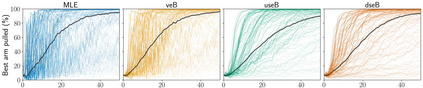
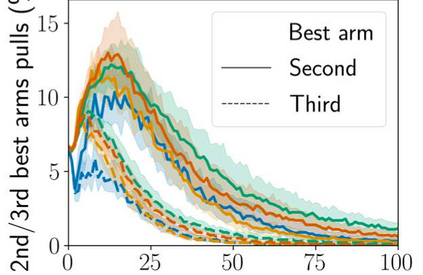
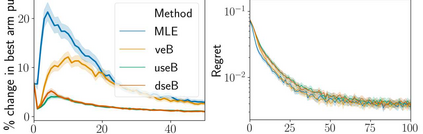
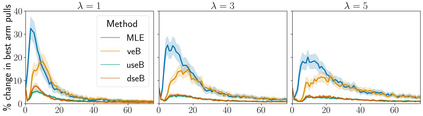
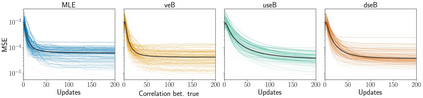
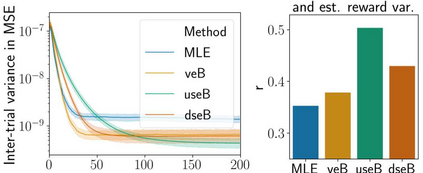
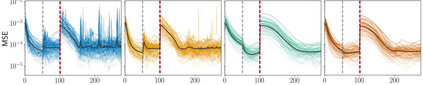
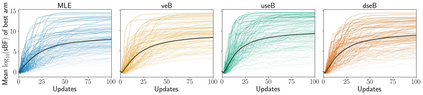
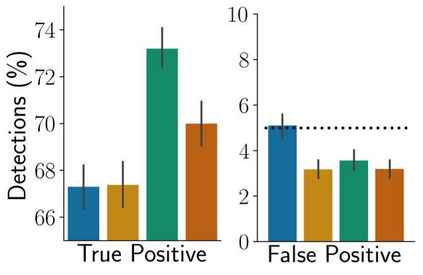
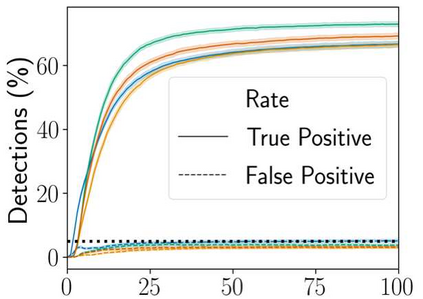
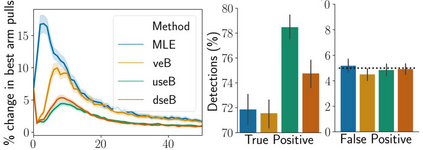
Stochastic delays in feedback lead to unstable sequential learning using multi-armed bandits. Recently, empirical Bayesian shrinkage has been shown to improve reward estimation in bandit learning. Here, we propose a novel adaptation to shrinkage that estimates smoothed reward estimates from windowed cumulative inputs, to deal with incomplete knowledge from delayed feedback and non-stationary rewards. Using numerical simulations, we show that this adaptation retains the benefits of shrinkage, and improves the stability of reward estimation by more than 50%. Our proposal reduces variability in treatment allocations to the best arm by up to 3.8x, and improves statistical accuracy - with up to 8% improvement in true positive rates and 37% reduction in false positive rates. Together, these advantages enable control of the trade-off between speed and stability of adaptation, and facilitate human-in-the-loop sequential optimisation.
翻译:通过多武装匪徒,反馈的拖延导致连续学习的不稳定。最近,经验型贝叶斯萎缩表明,在土匪学习中提高了奖励估计值。在这里,我们建议对从窗口累积投入中估算平滑的奖励估计数的缩减进行新颖的调整,处理来自延迟反馈和非静态奖励的不完整知识。我们利用数字模拟,表明这种调整保留了收缩的好处,提高了奖励估算的稳定性超过50 % 。 我们的建议将最佳手臂的治疗分配的变异性降低到3.8x,并提高统计准确性 — — 真实正率提高高达8%,假正率降低37%。 这些优势共同帮助控制了适应速度和稳定性之间的平衡,并促进了人与人之间的顺序优化。