False discovery proportion envelopes with consistency

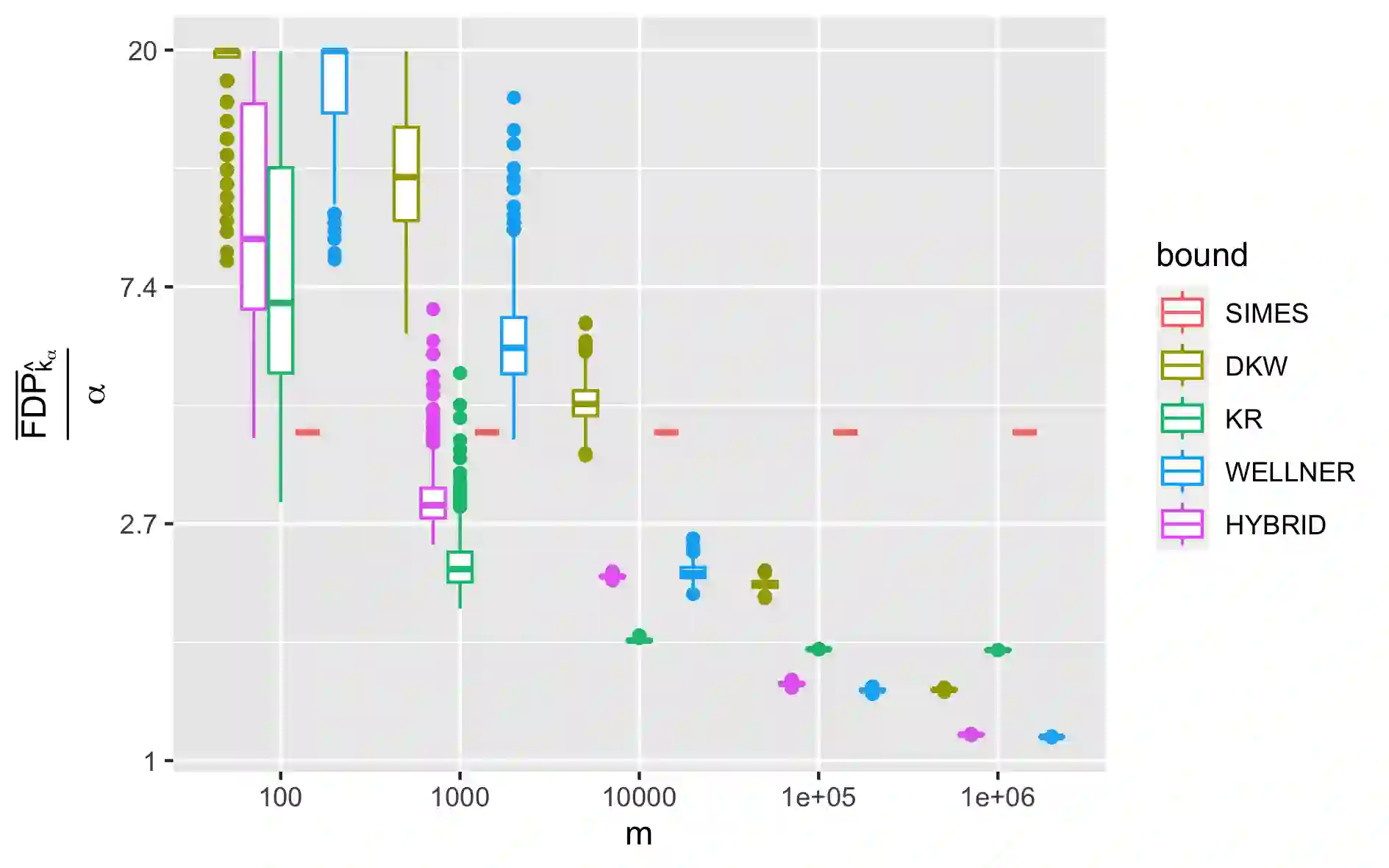
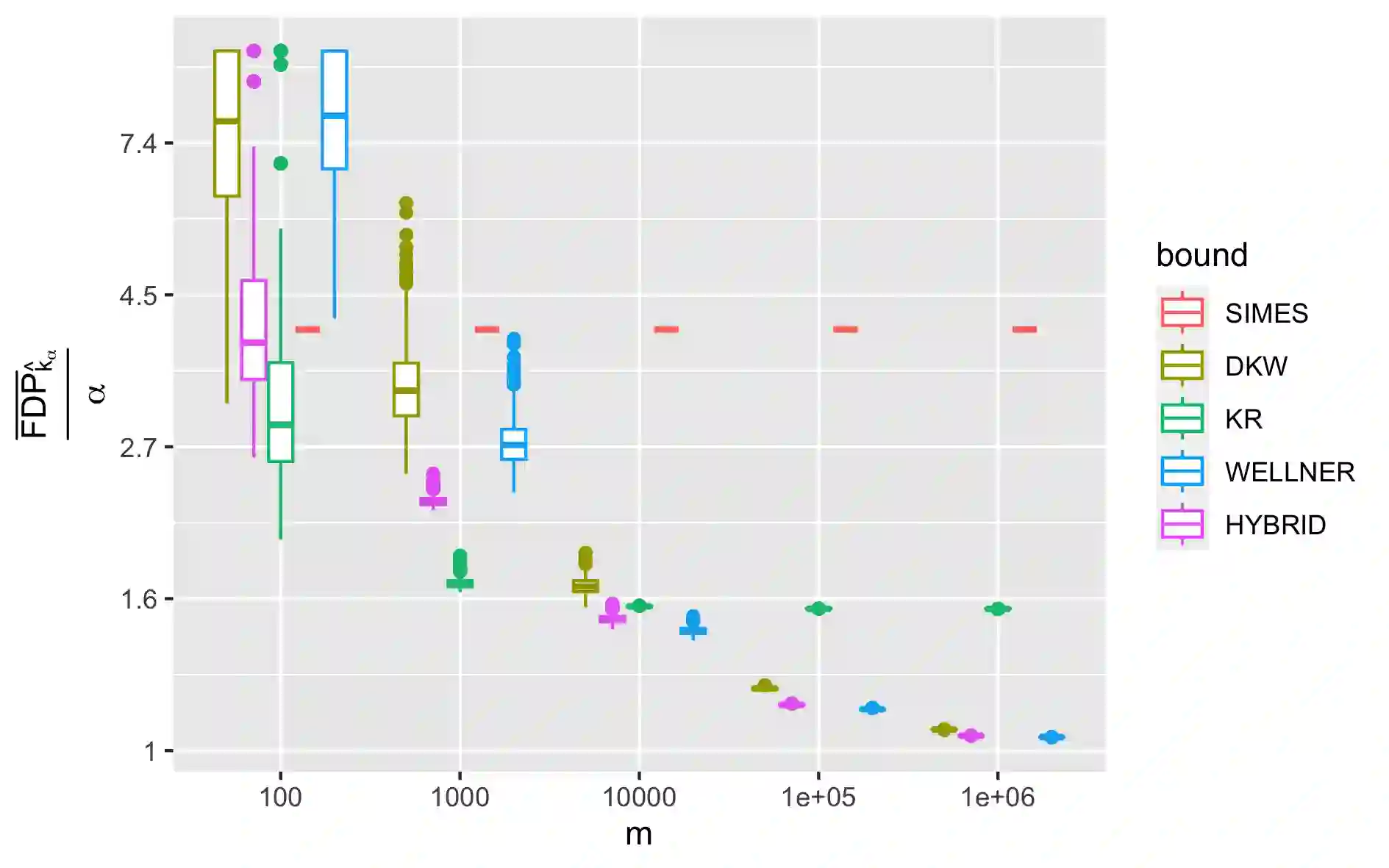
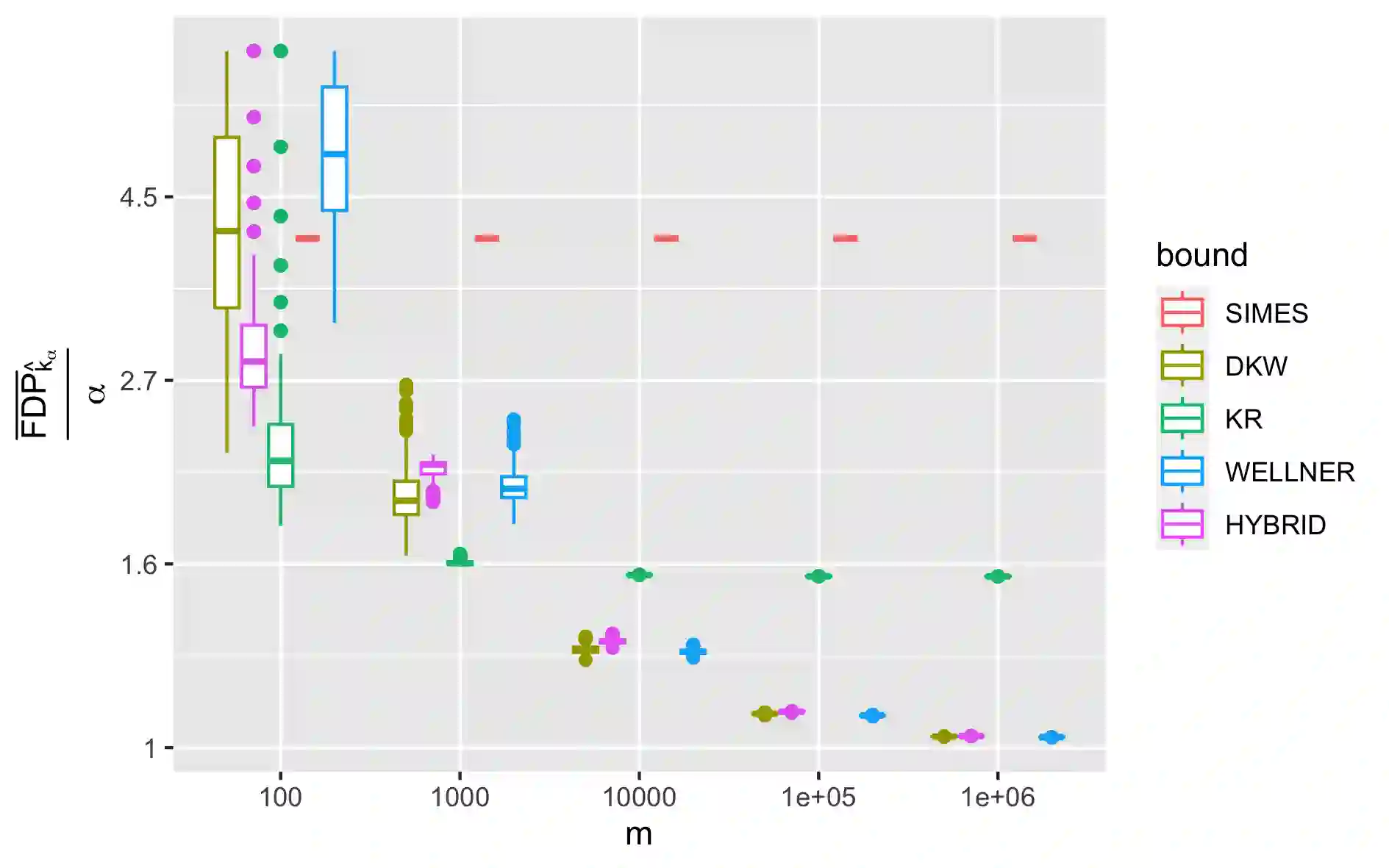
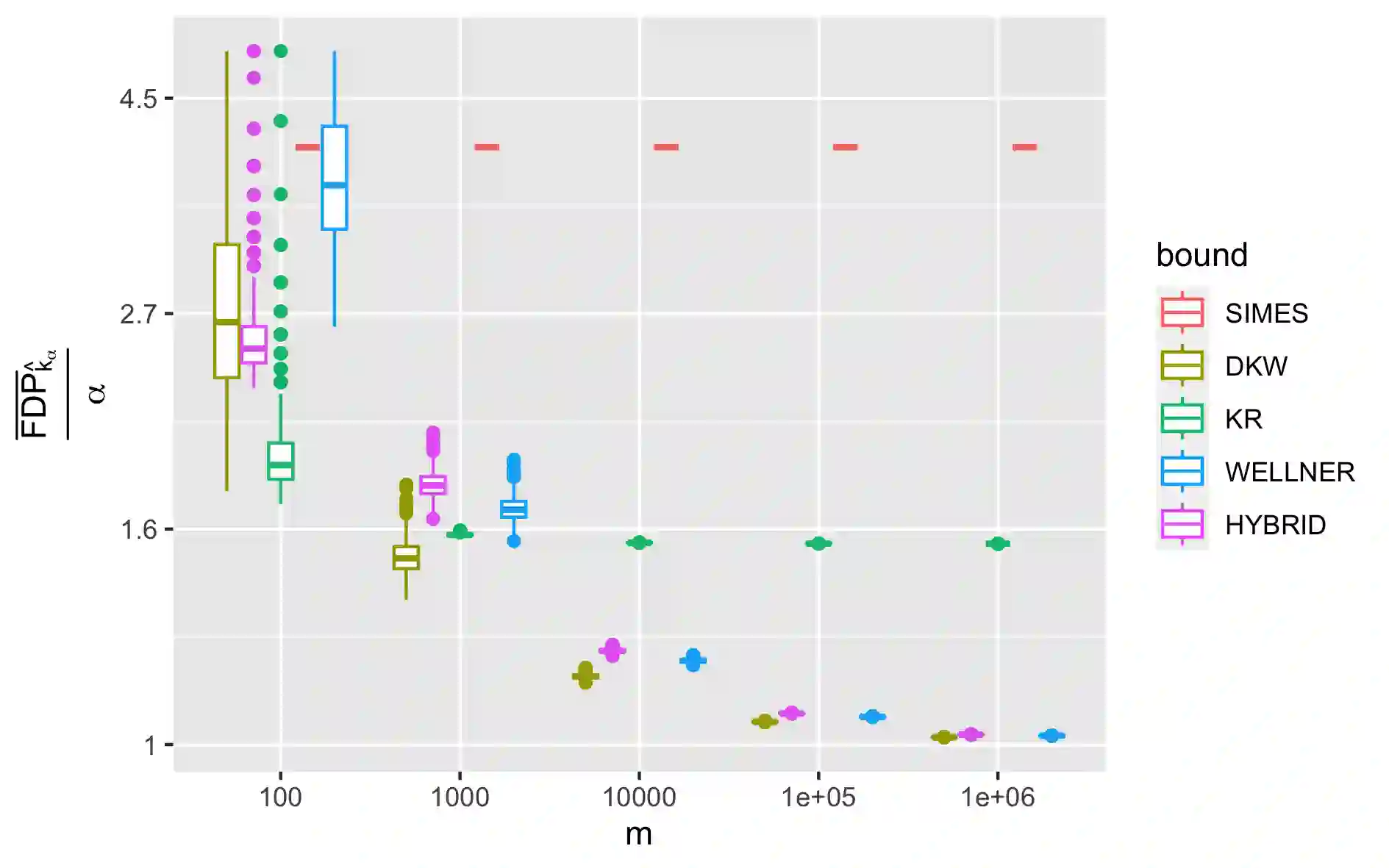
We provide new false discovery proportion (FDP) confidence envelopes in several multiple testing settings relevant to modern high dimensional-data methods. We revisit the scenarios considered in the recent work of \cite{katsevich2020simultaneous}(top-$k$, preordered -- including knockoffs -- , online) with a particular emphasis on obtaining FDP bounds that have both non-asymptotical coverage and asymptotical consistency, i.e. converge below the desired level $\alpha$ when applied to a classical $\alpha$-level false discovery rate (FDR) controlling procedure. This way, we derive new bounds that provide improvements over existing ones, both theoretically and practically, and are suitable for situations where at least a moderate number of rejections is expected. These improvements are illustrated with numerical experiments and real data examples. In particular, the improvement is significant in the knockoff setting, which shows the impact of the method for practical use. As side results, we introduce a new confidence envelope for the empirical cumulative distribution function of i.i.d. uniform variables and we provide new power results in sparse cases, both being of independent interest.