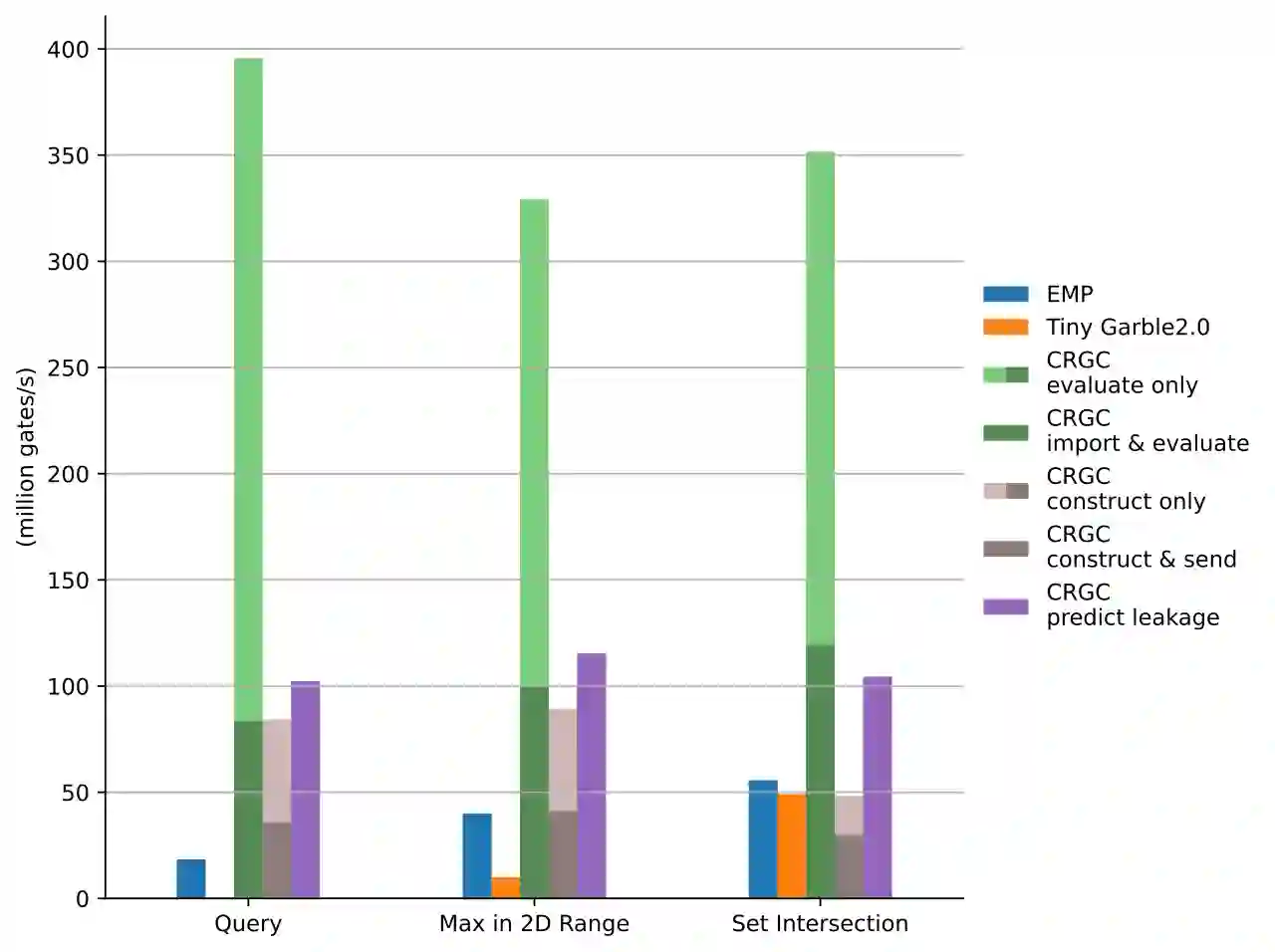
In this work, we introduce two schemes to construct reusable garbled circuits (RGCs) in the semi-honest setting. Our completely reusable garbled circuit (CRGC) scheme allows the generator (party A) to construct and send an obfuscated boolean circuit along with an encoded input to the evaluator (party B). In contrast to Yao's Garbled Circuit protocol, B can securely evaluate the same CRGC with an arbitrary number of inputs. As a tradeoff, CRGCs predictably leak some input bits of A to B. We also propose a partially reusable garbled circuit (PRGC) scheme that divides a circuit into reusable and non-reusable sections. PRGCs do not leak input bits of A. We benchmark our CRGC implementation against the state-of-the-art garbled circuit libraries EMP SH2PC and TinyGarble2. Using our framework, evaluating a CRGC is up to twenty times faster, albeit with weaker privacy guarantees, than evaluating an equivalent garbled circuit constructed by the two existing libraries. Our open-source library can convert any C++ function to a CRGC at approx. 80 million gates per second and repeatedly evaluate a CRGC at approx. 350 million gates per second. Additionally, a compressed CRGC is approx. 75% smaller in file size than the unobfuscated boolean circuit.
翻译:在这项工作中,我们引入了两种办法,在半光化环境下建造可再利用的加压电路。我们完全可再利用的加压电路(CRGC)方案允许发电机(A方)建造和发送一个模糊的布林电路,同时向评价员(B方)发送一个编码输入。与姚的加压电路协议相比,B可以任意地对同一CRGC进行数量投入的可靠评估。作为权衡,可预见地将A到B的一些输入点泄漏到B。我们还提议了一个部分可再利用的加压电路(CRGC)方案,将电路分为可再利用和不可再利用的部分。 与Yao的加压电路程序相比,B可以安全地对同一个CRGC系统进行评审。 与两个现有CRGC系统门的等同的平流电路路段相比,我们CRGC系统运行比80万CMC的CMCMA系统要反复评估了20万次。