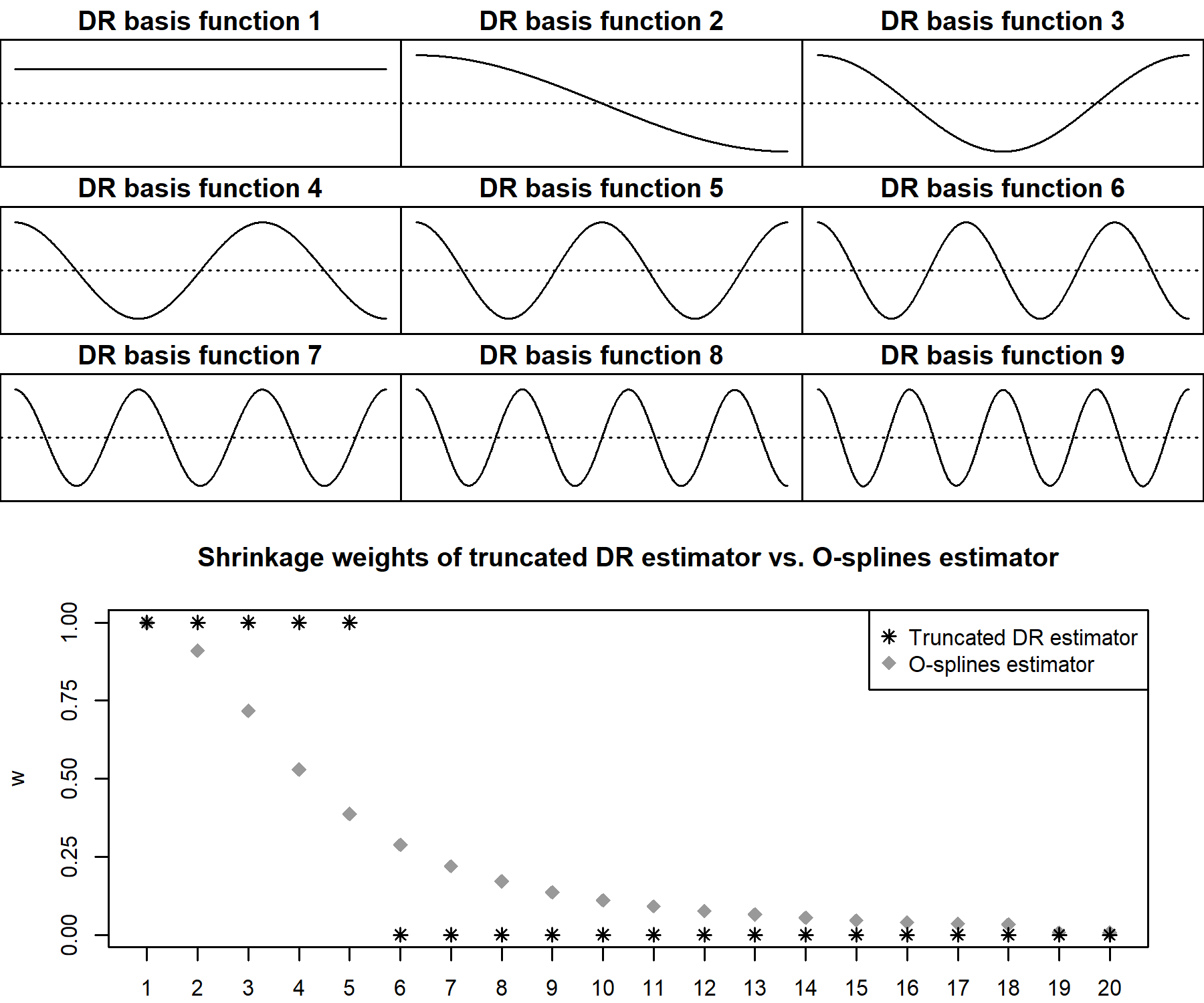
Despite their widespread use in practice, the asymptotic properties of Bayesian penalized splines have not been investigated so far. We close this gap and study posterior concentration rates for Bayesian penalized splines in a Gaussian nonparametric regression model. A key feature of the approach is the hyperprior on the smoothing variance, which allows for adaptive smoothing in practice but complicates the theoretical analysis considerably. Our main tool for the derivation of posterior concentration rates with a general hyperprior on the smoothing variance is a novel spline estimator that projects the observations onto the first basis functions of a Demmler-Reinsch basis. Our results show that posterior concentration at near optimal rate can be achieved if the hyperprior on the smoothing variance strikes a fine balance between oversmoothing and undersmoothing. Another interesting finding is that the order of the roughness penalty must exactly match the regularity of the unknown regression function in order to achieve posterior concentration at near optimal rate. Overall, our results are the first posterior concentration results for Bayesian penalized splines and can be generalized in many directions.
翻译:尽管在实际中广泛使用,但至今尚未调查贝耶斯州受惩罚的样条的无症状特性。我们缩小了这一差距并研究了巴伊西亚州受惩罚的样条在高斯州非参数回归模型中的后表浓度率。这一方法的一个关键特征是,平滑差异的高度重要性,这在实际中允许适应性平滑,但使理论分析大为复杂化。我们得出后表层集中率的主要工具与平滑差异方面的一般超强作用完全吻合,这是一个新的样板估计器,将观测结果投射到Demmler-Reinsch基础的第一个基础函数上。我们的结果显示,如果平滑差异的超优等在悬浮和下悬浮之间取得细微平衡,后表集中率可以接近最佳的速度达到。另一个有趣的发现是,粗糙惩罚的顺序必须与未知的回归功能的规律性完全吻合,以便以近最佳的速度实现后表集中。总体而言,我们的结果是巴伊西亚州受惩罚的样板条纹的样板条形板块的最初后部浓度结果。