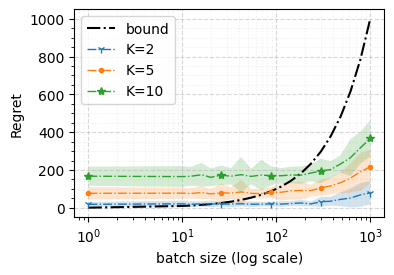
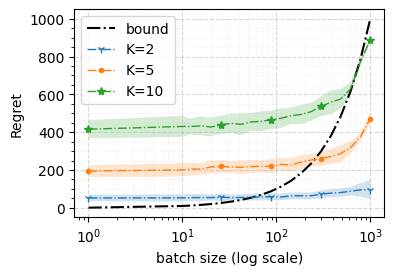
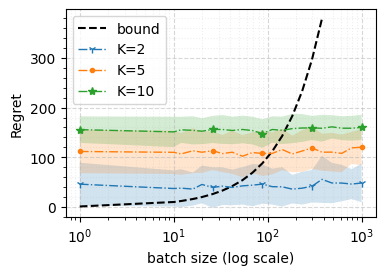
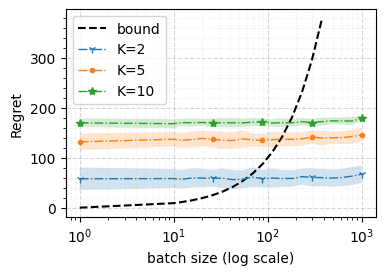
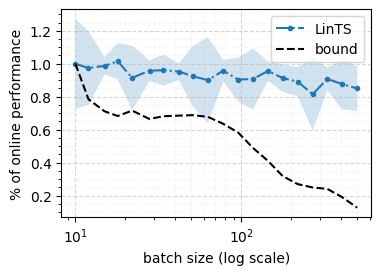
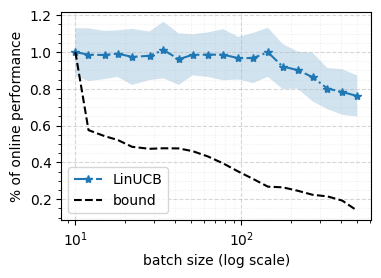
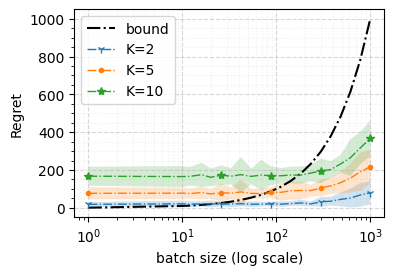
We consider a special case of bandit problems, named batched bandits, in which an agent observes batches of responses over a certain time period. Unlike previous work, we consider a more practically relevant batch-centric scenario of batch learning. That is to say, we provide a policy-agnostic regret analysis and demonstrate upper and lower bounds for the regret of a candidate policy. Our main theoretical results show that the impact of batch learning is a multiplicative factor of batch size relative to the regret of online behavior. Primarily, we study two settings of the stochastic linear bandits: bandits with finitely and infinitely many arms. While the regret bounds are the same for both settings, the former setting results hold under milder assumptions. Also, we provide a more robust result for the 2-armed bandit problem as an important insight. Finally, we demonstrate the consistency of theoretical results by conducting empirical experiments and reflect on optimal batch size choice.
翻译:我们考虑的是土匪问题的特殊案例,称为分批强盗,其中一名代理人在一段时间内观察了成批的响应。与以前的工作不同,我们考虑的是更切合实际的分批学习的批量中心情景。也就是说,我们提供政策上不可知的遗憾分析,并展示对候选政策遗憾的上下界限。我们的主要理论结果显示,批量学习的影响是批量规模与在线行为的遗憾相比的倍数倍增因素。我们主要研究的是两个随机线性强盗的设置:带有限和无限多手臂的土匪。虽然这两种情况下的遗憾界限相同,但前者在较温和的假设下可以维持结果。此外,我们还为2架土匪问题提供了更强有力的结果,作为重要的见解。最后,我们通过进行实验实验和思考最佳的批量选择,来证明理论结果的一致性。