Koopman operators with intrinsic observables in rigged reproducing kernel Hilbert spaces

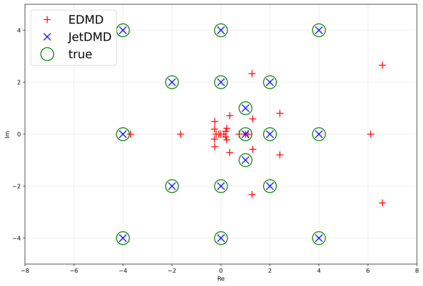
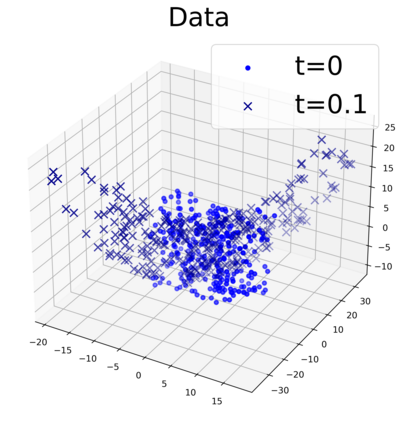
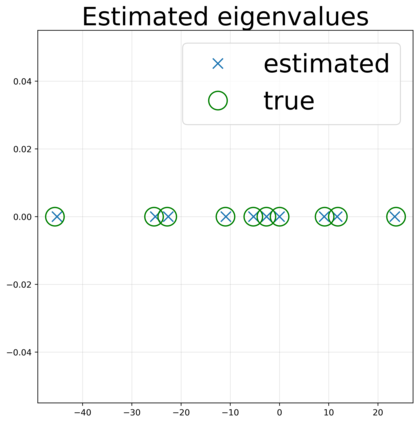
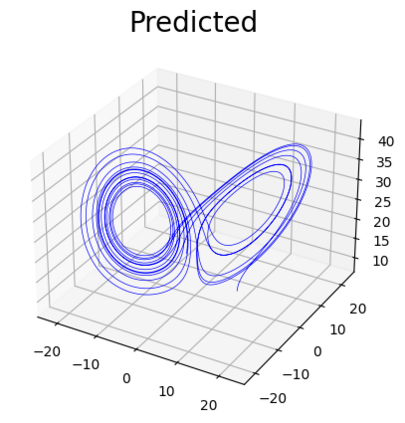
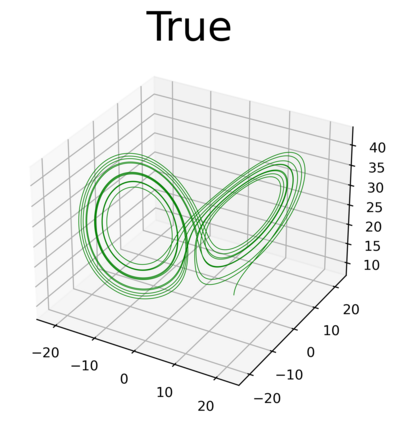
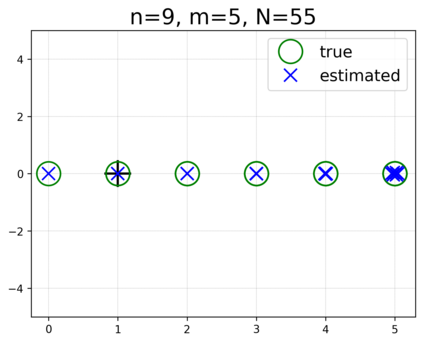
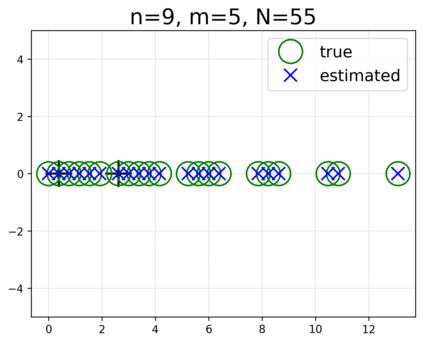
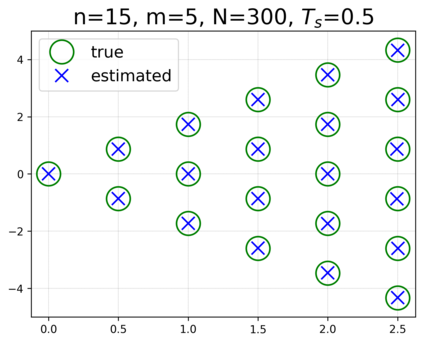
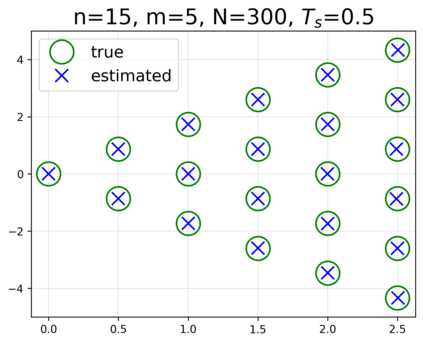
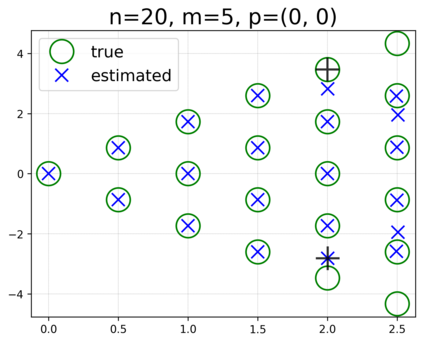
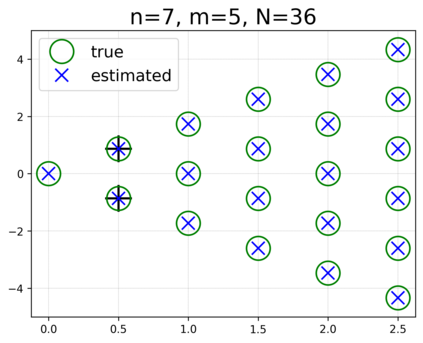
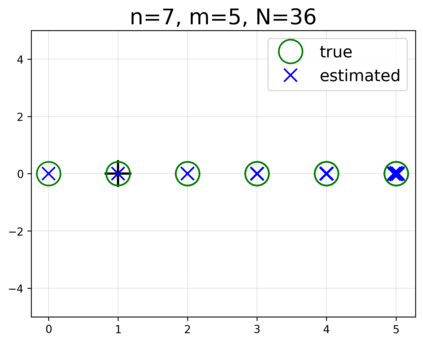
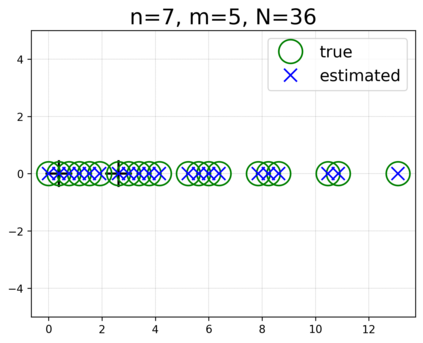
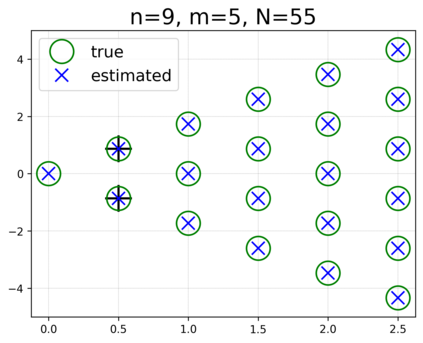
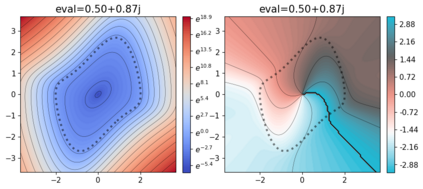
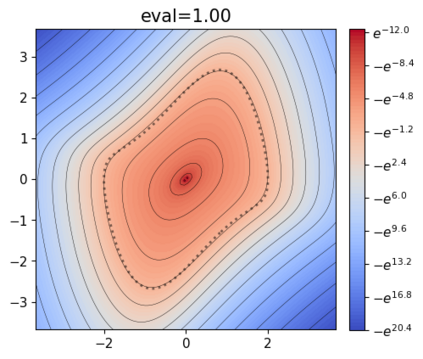
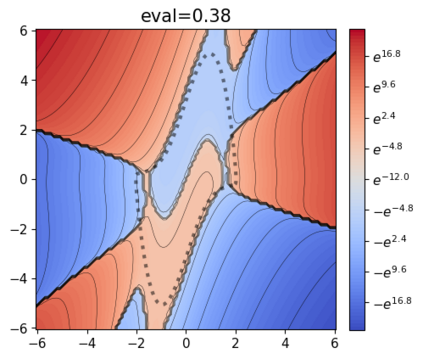
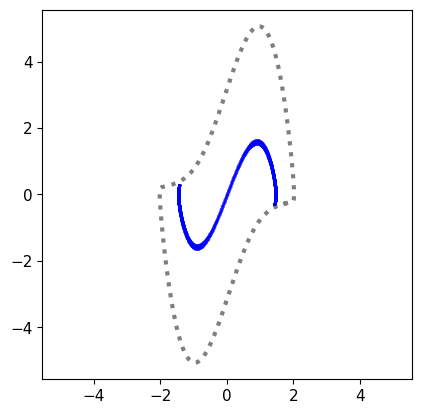
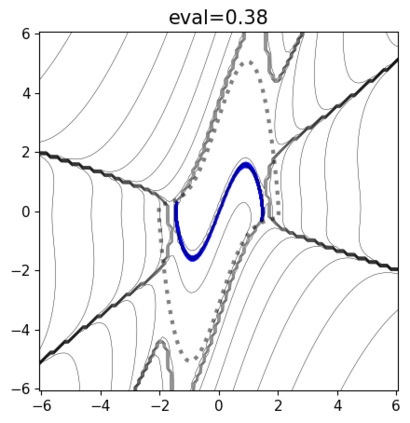
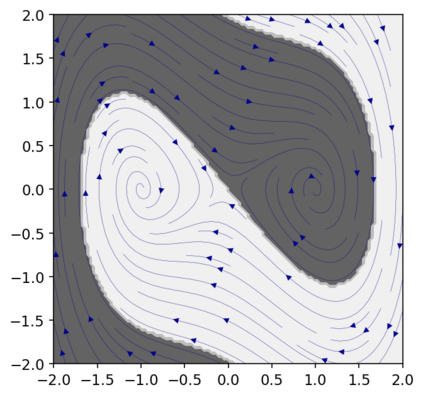
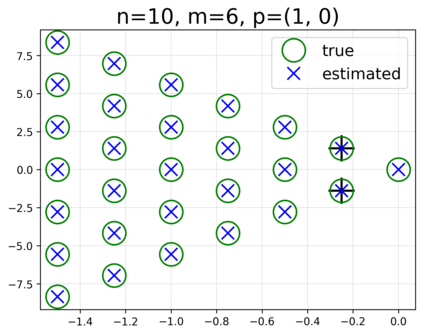
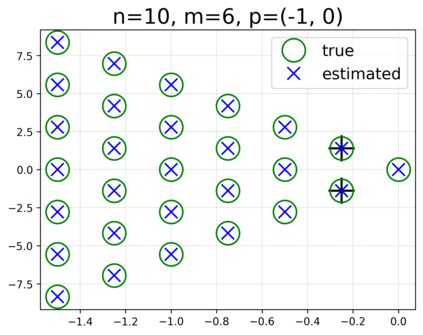
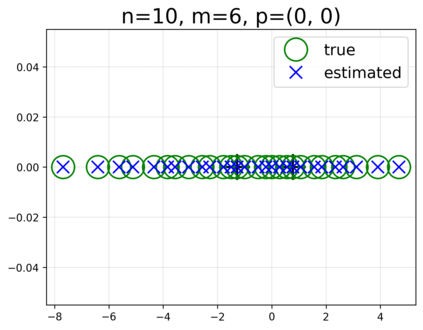
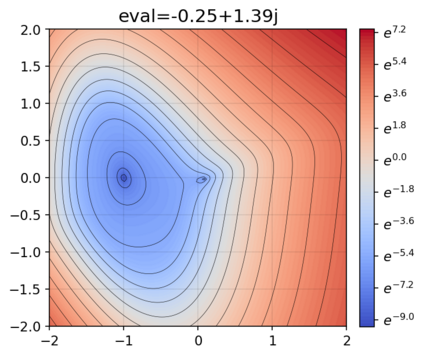
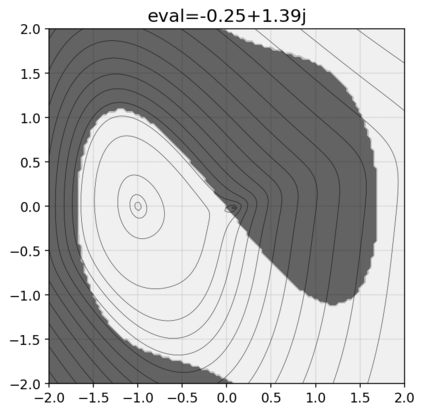
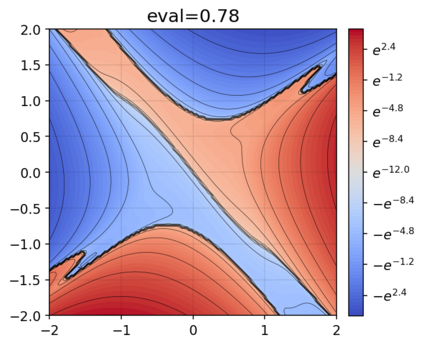
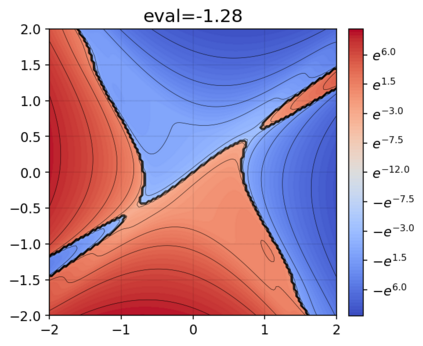
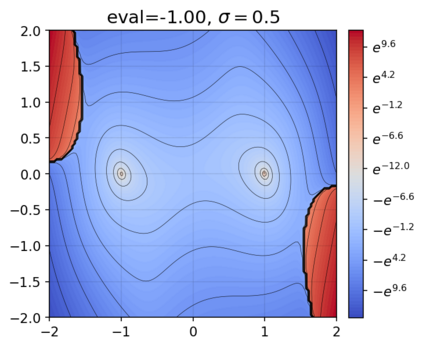
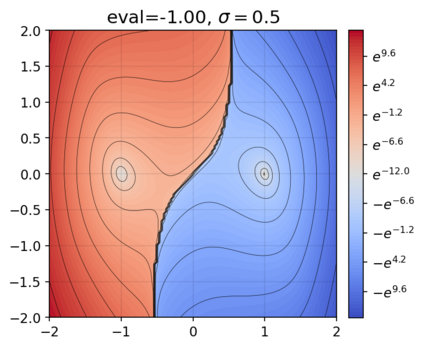
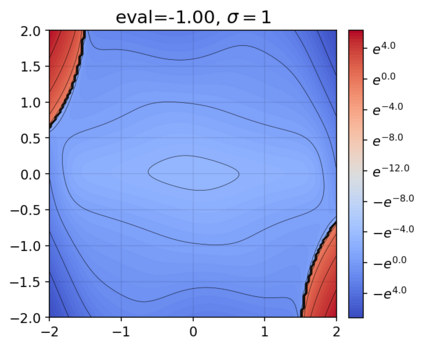
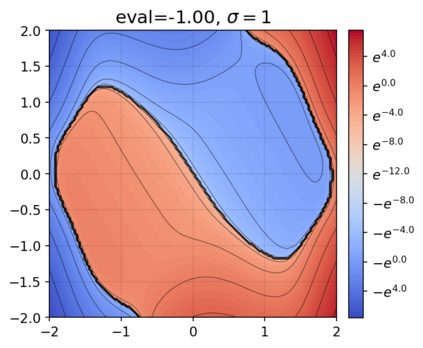
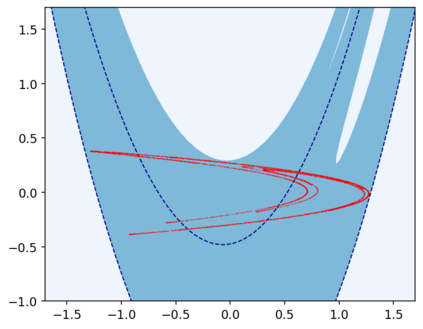
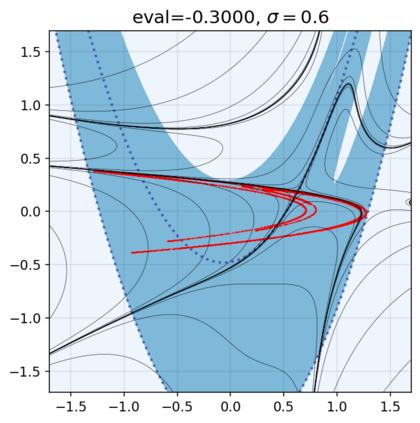
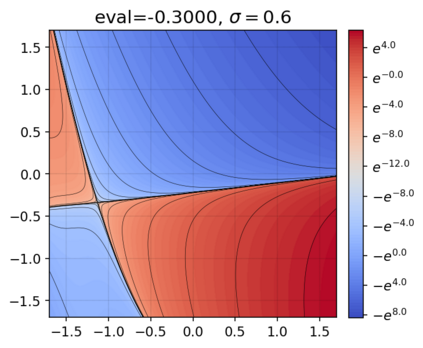
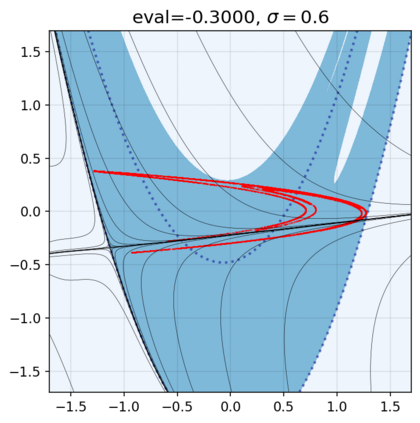
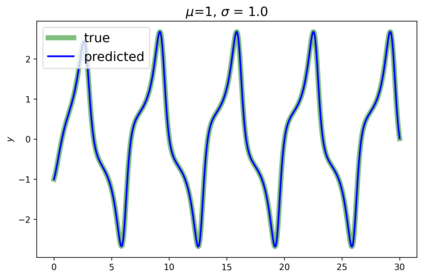
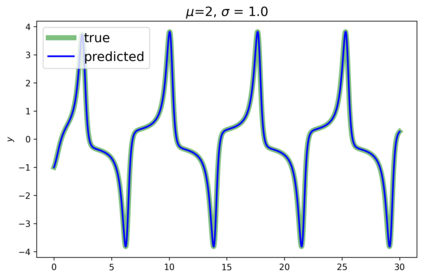
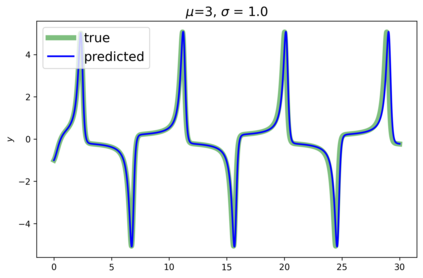
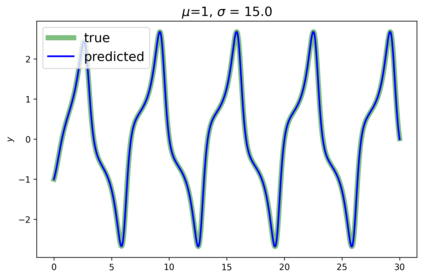
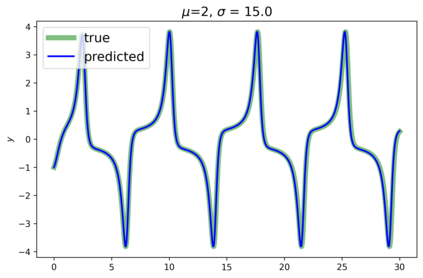
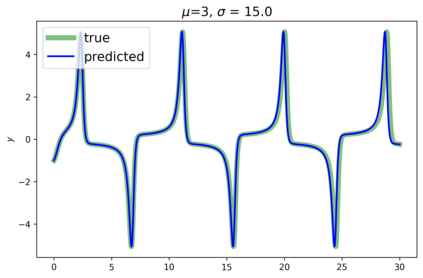
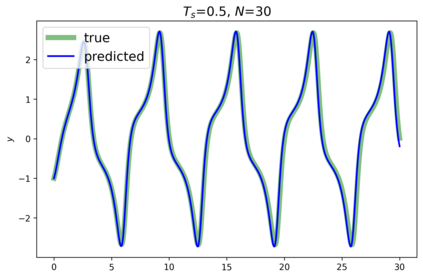
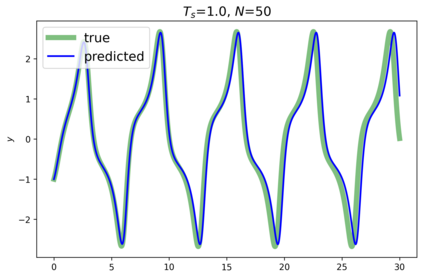
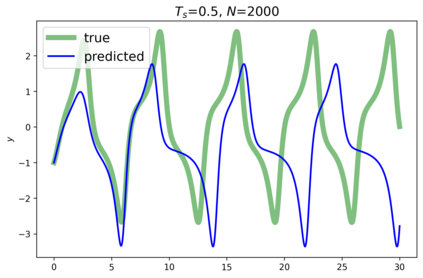
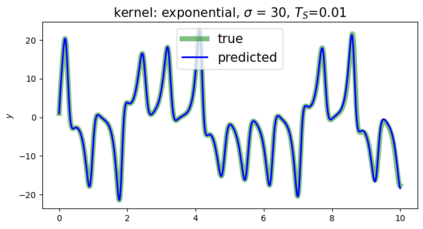
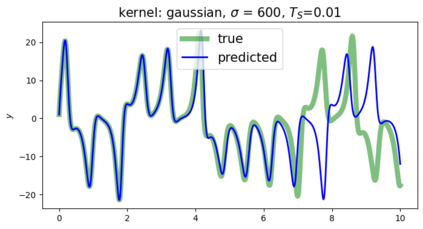
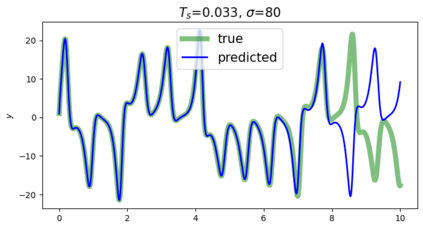
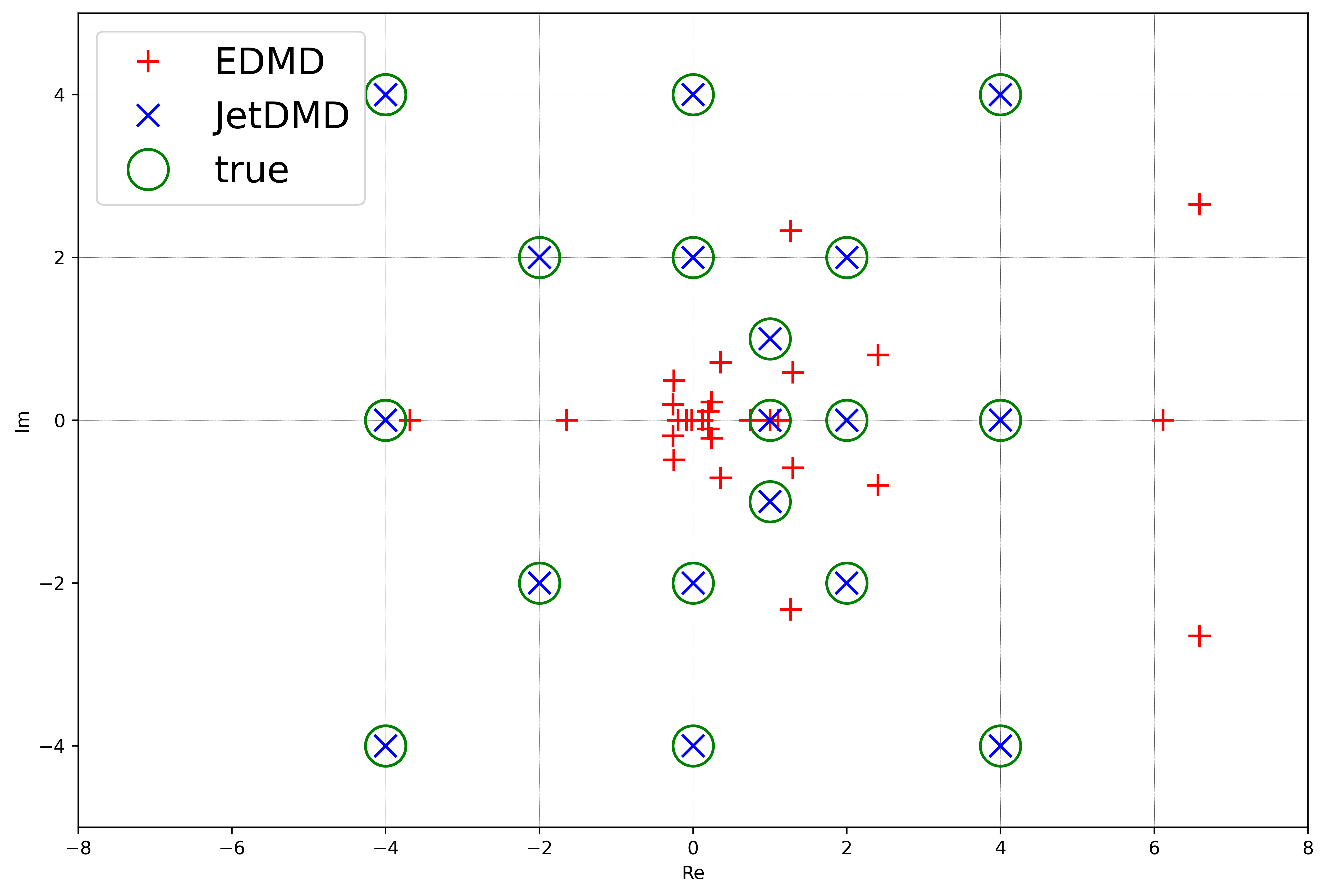
This paper presents a novel approach for estimating the Koopman operator defined on a reproducing kernel Hilbert space (RKHS) and its spectra. We propose an estimation method, what we call Jet Dynamic Mode Decomposition (JetDMD), leveraging the intrinsic structure of RKHS and the geometric notion known as jets to enhance the estimation of the Koopman operator. This method refines the traditional Extended Dynamic Mode Decomposition (EDMD) in accuracy, especially in the numerical estimation of eigenvalues. This paper proves JetDMD's superiority through explicit error bounds and convergence rate for special positive definite kernels, offering a solid theoretical foundation for its performance. We also delve into the spectral analysis of the Koopman operator, proposing the notion of extended Koopman operator within a framework of rigged Hilbert space. This notion leads to a deeper understanding of estimated Koopman eigenfunctions and capturing them outside the original function space. Through the theory of rigged Hilbert space, our study provides a principled methodology to analyze the estimated spectrum and eigenfunctions of Koopman operators, and enables eigendecomposition within a rigged RKHS. We also propose a new effective method for reconstructing the dynamical system from temporally-sampled trajectory data of the dynamical system with solid theoretical guarantee. We conduct several numerical simulations using the van der Pol oscillator, the Duffing oscillator, the H\'enon map, and the Lorenz attractor, and illustrate the performance of JetDMD with clear numerical computations of eigenvalues and accurate predictions of the dynamical systems.