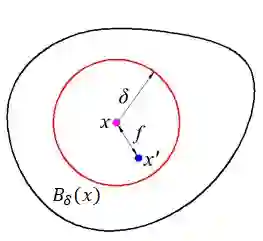
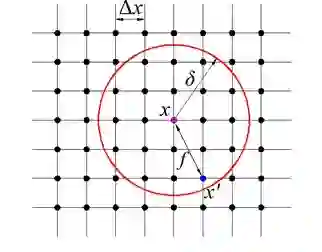
Peridynamics is a nonlocal theory for dynamic fracture analysis consisting in a second order in time partial integro-differential equation. In this paper, we consider a nonlinear model of peridynamics in a two-dimensional spatial domain. We implement a spectral method for the space discretization based on the Fourier expansion of the solution while we consider the Newmark-$\beta$ method for the time marching. This computational approach takes advantages from the convolutional form of the peridynamic operator and from the use of the discrete Fourier transform. We show a convergence result for the fully discrete approximation and study the stability of the method applied to the linear peridynamic model. Finally, we perform several numerical tests and comparisons to validate our results and provide simulations implementing a volume penalization technique to avoid the limitation of periodic boundary conditions due to the spectral approach.
翻译:周围动力学是动态断裂分析的非局部理论,它以时间顺序的第二顺序构成局部分化等式。在本文中,我们考虑了二维空间领域的非线性极动力学模型。我们采用基于Fourier扩大溶液的空间分解光谱法,而我们则考虑用Newmark-$\beeta$的方法进行时间进化。这种计算方法利用了渗透动力操作员的分流形式和使用离散的Fourier变异法的优势。我们显示了完全离散近似的趋同结果,并研究了线性极动力学模型所用方法的稳定性。最后,我们进行了数个数字测试和比较,以验证我们的结果,并提供模拟,采用数量惩罚法,以避免由于光谱方法而限制定期边界条件。