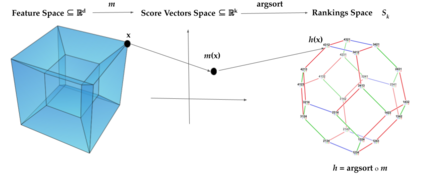
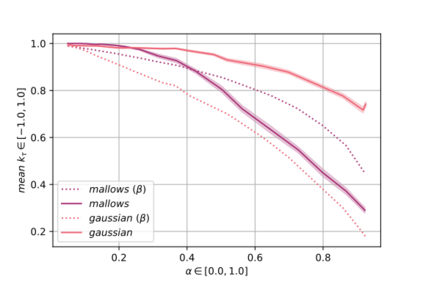
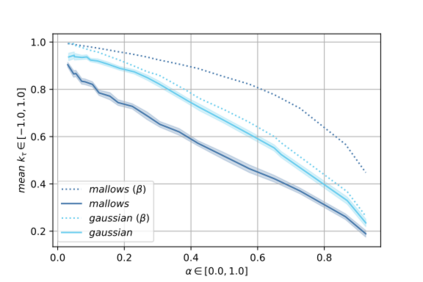
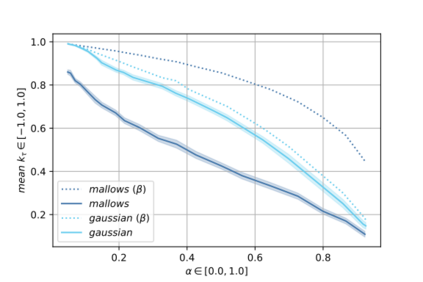
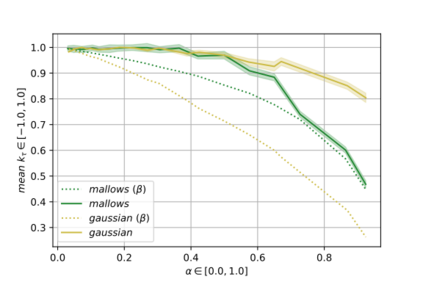
Label Ranking (LR) corresponds to the problem of learning a hypothesis that maps features to rankings over a finite set of labels. We adopt a nonparametric regression approach to LR and obtain theoretical performance guarantees for this fundamental practical problem. We introduce a generative model for Label Ranking, in noiseless and noisy nonparametric regression settings, and provide sample complexity bounds for learning algorithms in both cases. In the noiseless setting, we study the LR problem with full rankings and provide computationally efficient algorithms using decision trees and random forests in the high-dimensional regime. In the noisy setting, we consider the more general cases of LR with incomplete and partial rankings from a statistical viewpoint and obtain sample complexity bounds using the One-Versus-One approach of multiclass classification. Finally, we complement our theoretical contributions with experiments, aiming to understand how the input regression noise affects the observed output.
翻译:label Ranging (LR) 与学习以下假设的问题相对应: 学习一种假设,该假设在一定标签组的排名中绘制特征; 我们对LR采取非参数回归法,并获得这一基本实际问题的理论性能保障; 我们引入了无噪音和吵闹的非参数回归情况下的Label Ranging 的基因模型, 并为这两种情况下的学习算法提供了样本复杂性界限; 在无噪音环境下, 我们用完全排序来研究LLR问题, 并利用决定树和高维系统中的随机森林提供计算效率的算法。 在吵闹的环境下, 我们从统计角度考虑LR的不完全和部分排名的比较一般案例, 并使用多级分类的一Versus-One方法获得样本复杂性界限。 最后, 我们用实验来补充我们的理论贡献, 目的是了解输入回归噪音如何影响观察到的产出。