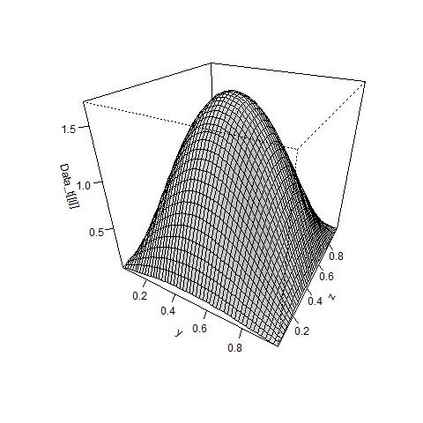
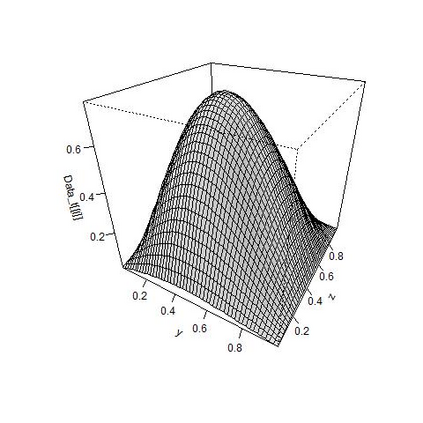
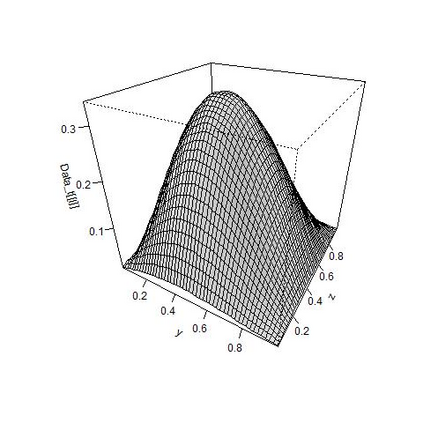
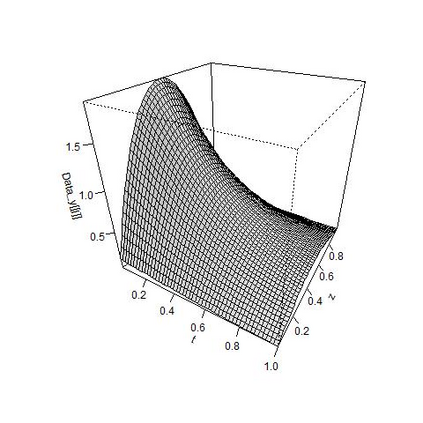
We study parameter estimation for a linear parabolic second-order stochastic partial differential equation (SPDE) in two space dimensions with a small dispersion parameter using high frequency data with respect to time and space. We set two types of $Q$-Wiener processes as a driving noise. We provide minimum contrast estimators of the coefficient parameters of the SPDE appearing in the coordinate process of the SPDE based on the thinned data in space, and approximate the coordinate process based on the thinned data in time. Moreover, we propose an estimator of the drift parameter using the fact that the coordinate process is the Ornstein-Uhlenbeck process and statistical inference for diffusion processes with a small noise.
翻译:我们利用时间和空间方面的高频数据研究两个空间维度的线性抛射二级局部偏差方程式的参数估计,其中使用时间和空间方面的高频数据进行小分散参数;我们将两种“Q$-Wiener”过程定为驱动噪音;我们根据空间中的稀薄数据提供SPDE协调过程中出现的SPDE系数参数的最小对比估计器,并根据时间上的稀薄数据对协调过程进行近似;此外,我们提议使用协调过程是Ornstein-Uhlenbeck过程和小噪音扩散过程的统计推论来估计漂移参数。