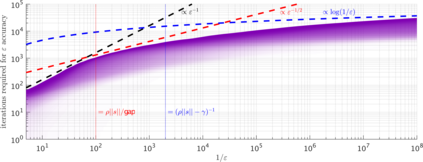
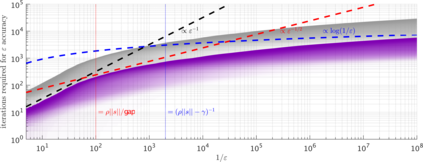
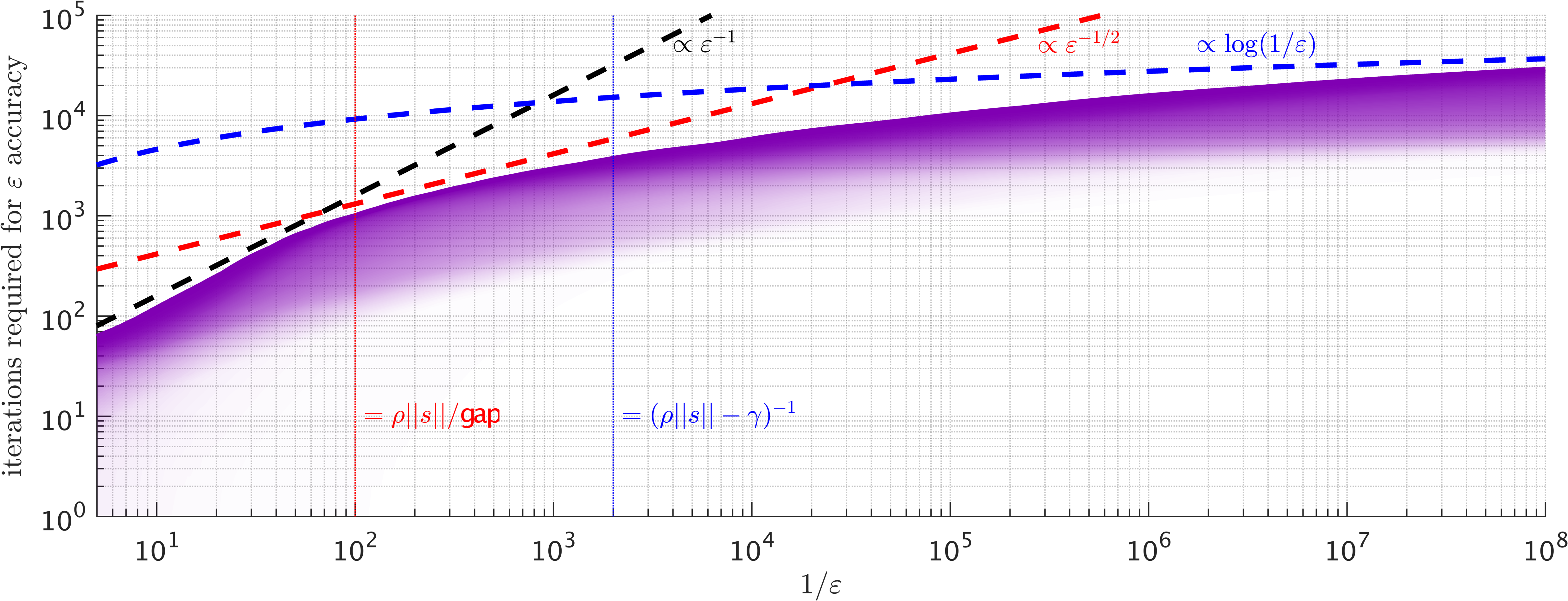
We consider the minimization of non-convex quadratic forms regularized by a cubic term, which exhibit multiple saddle points and poor local minima. Nonetheless, we prove that, under mild assumptions, gradient descent approximates the $\textit{global minimum}$ to within $\varepsilon$ accuracy in $O(\varepsilon^{-1}\log(1/\varepsilon))$ steps for large $\varepsilon$ and $O(\log(1/\varepsilon))$ steps for small $\varepsilon$ (compared to a condition number we define), with at most logarithmic dependence on the problem dimension. When we use gradient descent to approximate the cubic-regularized Newton step, our result implies a rate of convergence to second-order stationary points of general smooth non-convex functions.
翻译:我们考虑将非convex四边形形式通过一个立方任期正规化的最小化,这表现为多个马鞍点和当地微粒条件差。然而,我们证明,在轻度假设下,梯度下降大约等于美元(textit{global minutes),精确到美元(varepsilon)1 ⁇ (1/\varepsilon))美元(美元)和美元(log(1/\ varepsilon))美元(美元),小价(瓦列普斯隆)美元(与我们定义的条件数相比),在多数情况下,对问题层面有逻辑依赖。当我们使用梯度下降以接近立方正的牛顿步骤时,我们的结果意味着与一般平滑的非凝固功能的第二阶定点的趋同速度。