An interface-tracking space-time hybridizable/embedded discontinuous Galerkin method for nonlinear free-surface flows

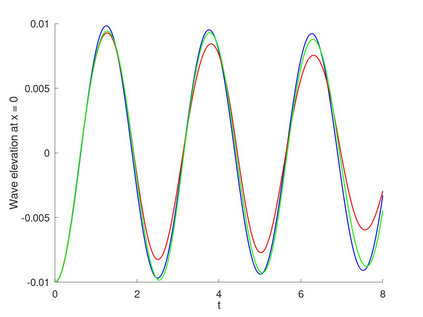
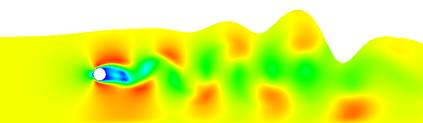
We present a compatible space-time hybridizable/embedded discontinuous Galerkin discretization for nonlinear free-surface waves. We pose this problem in a two-fluid (liquid and gas) domain and use a time-dependent level-set function to identify the sharp interface between the two fluids. The incompressible two-fluidd equations are discretized by an exactly mass conserving space-time hybridizable discontinuous Galerkin method while the level-set equation is discretized by a space-time embedded discontinuous Galerkin method. Different from alternative discontinuous Galerkin methods is that the embedded discontinuous Galerkin method results in a continuous approximation of the interface. This, in combination with the space-time framework, results in an interface-tracking method without resorting to smoothing techniques or additional mesh stabilization terms.