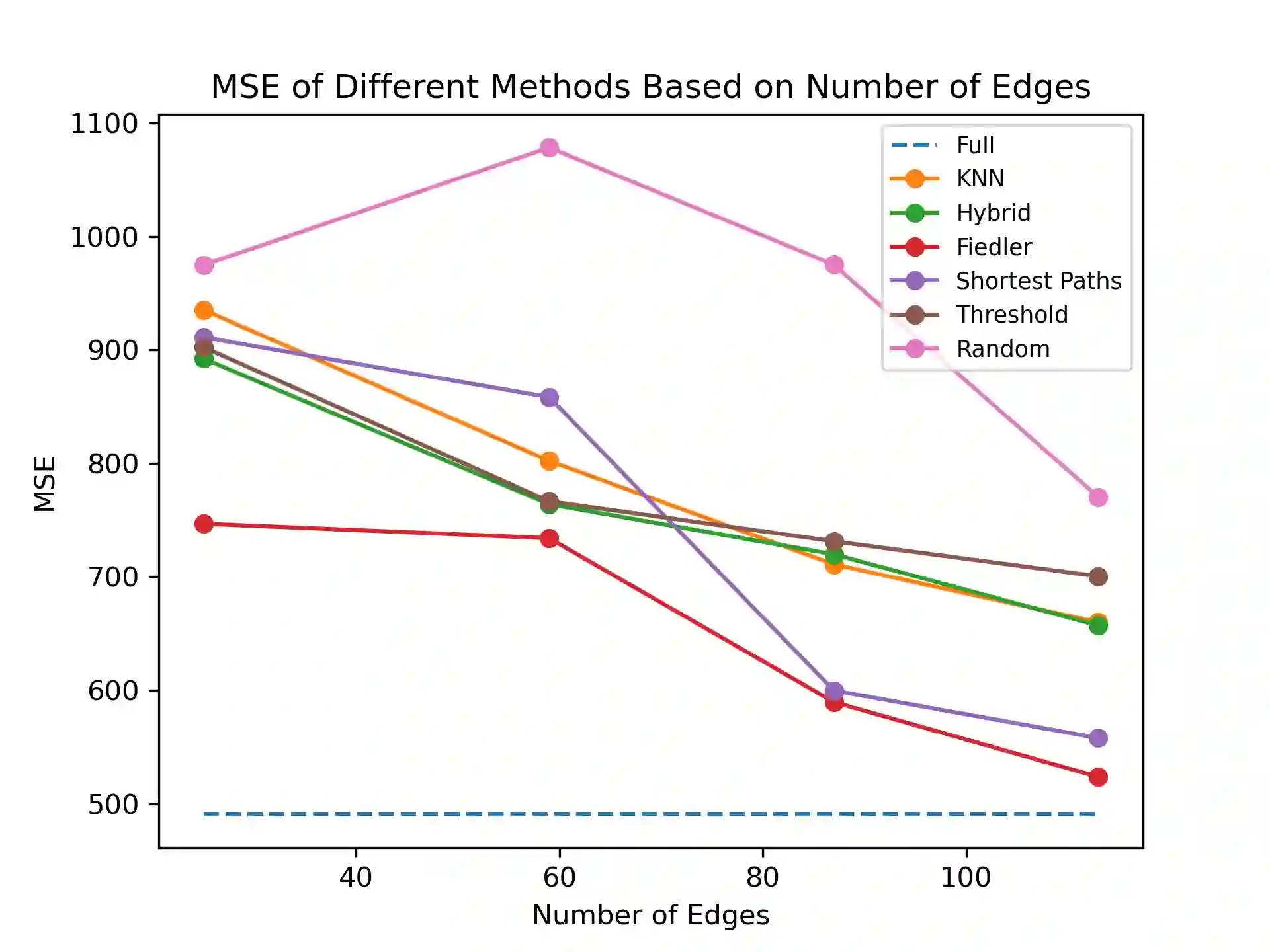
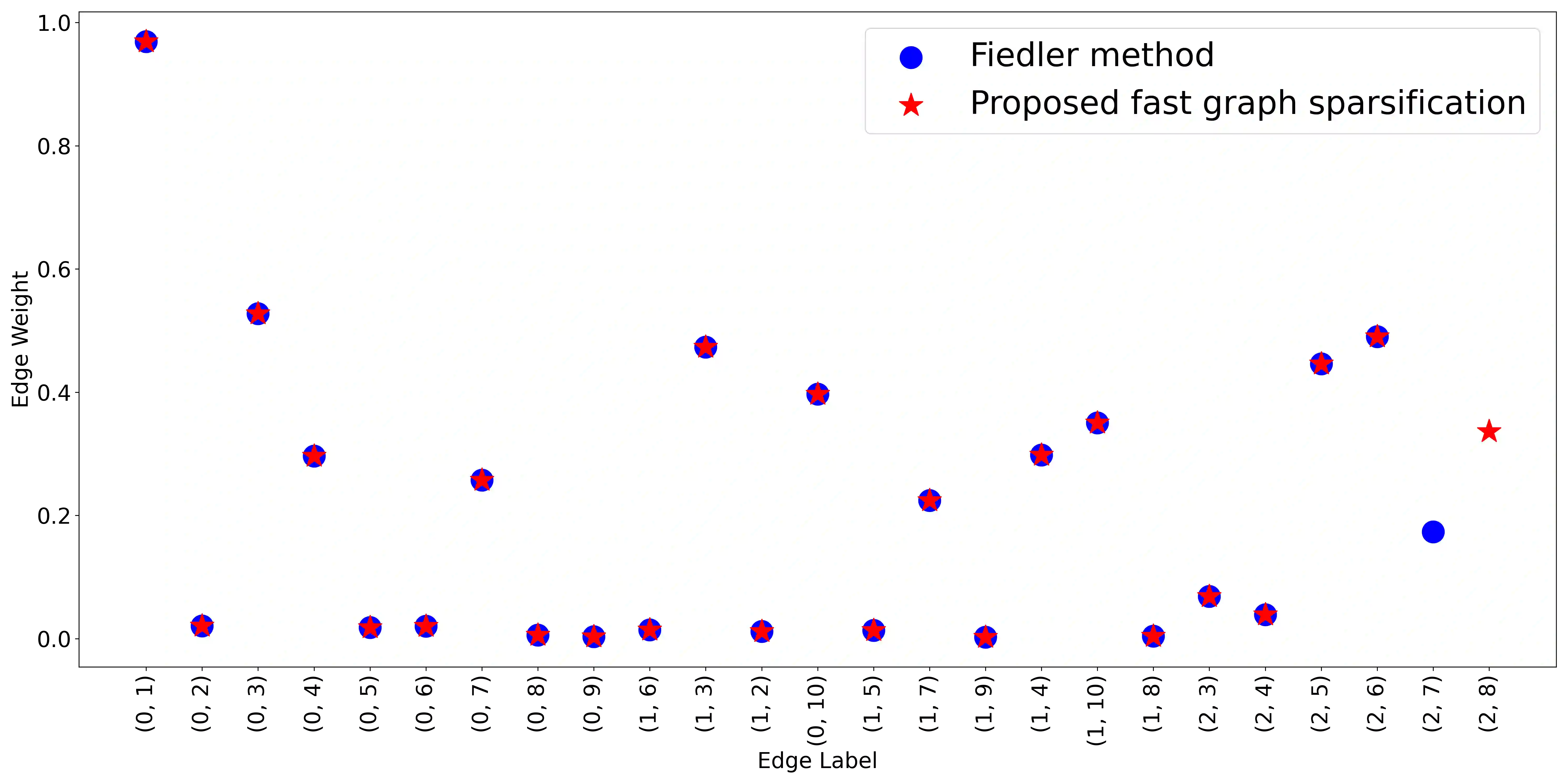
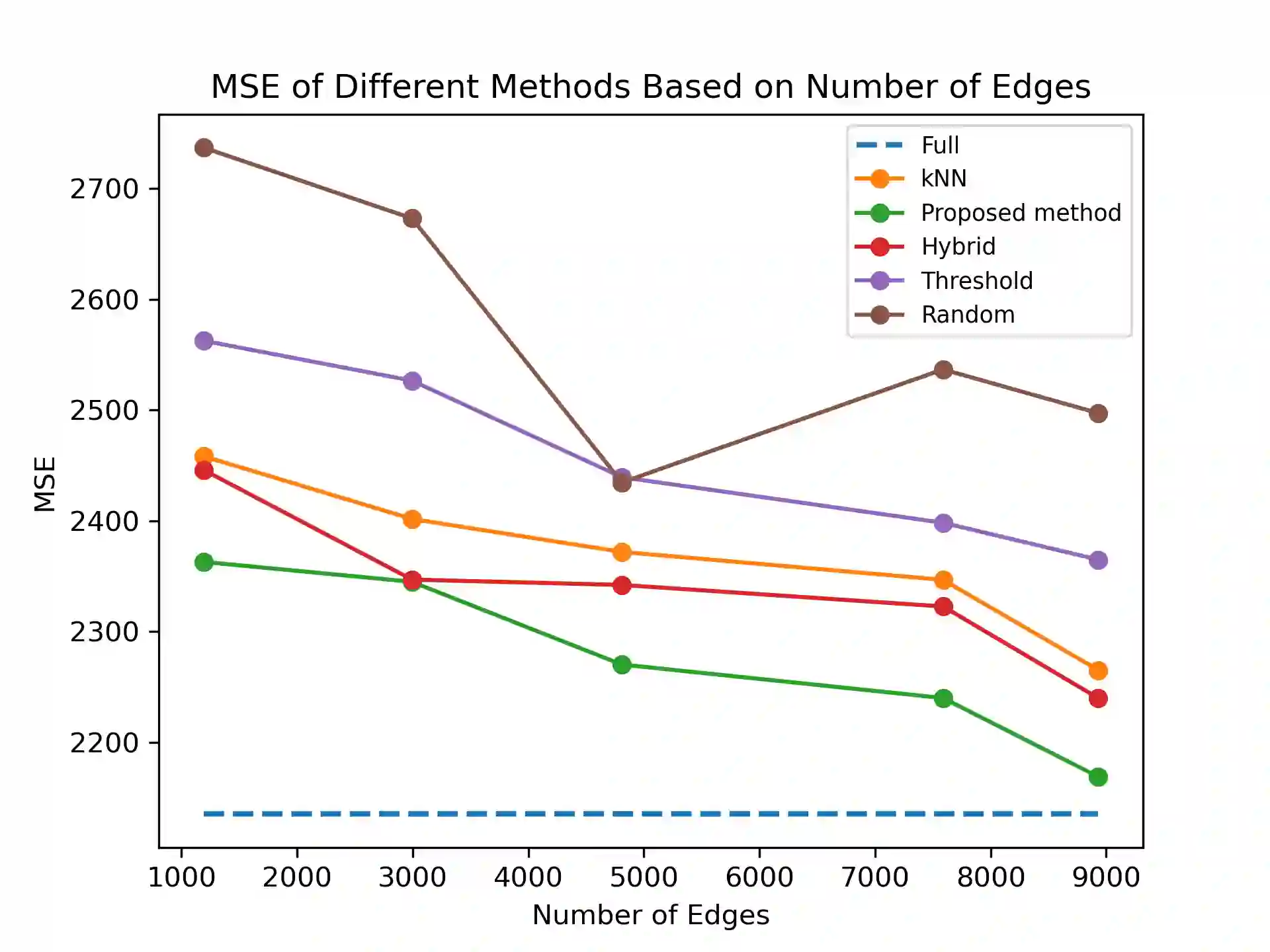
In agronomics, predicting crop yield at a per field/county granularity is important for farmers to minimize uncertainty and plan seeding for the next crop cycle. While state-of-the-art prediction techniques employ graph convolutional nets (GCN) to predict future crop yields given relevant features and crop yields of previous years, a dense underlying graph kernel requires long training and execution time. In this paper, we propose a graph sparsification method based on the Fiedler number to remove edges from a complete graph kernel, in order to lower the complexity of GCN training/execution. Specifically, we first show that greedily removing an edge at a time that induces the minimal change in the second eigenvalue leads to a sparse graph with good GCN performance. We then propose a fast method to choose an edge for removal per iteration based on an eigenvalue perturbation theorem. Experiments show that our Fiedler-based method produces a sparse graph with good GCN performance compared to other graph sparsification schemes in crop yield prediction.
翻译:暂无翻译