Multivariate Analysis for Multiple Network Data via Semi-Symmetric Tensor PCA

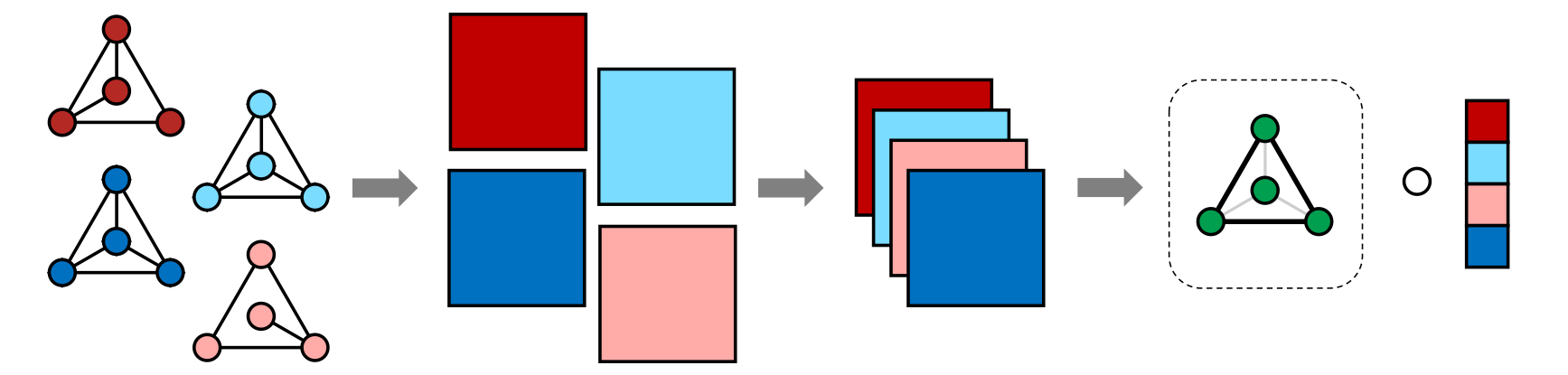
Network data are commonly collected in a variety of applications, representing either directly measured or statistically inferred connections between features of interest. In an increasing number of domains, these networks are collected over time, such as interactions between users of a social media platform on different days, or across multiple subjects, such as in multi-subject studies of brain connectivity. When analyzing multiple large networks, dimensionality reduction techniques are often used to embed networks in a more tractable low-dimensional space. To this end, we develop a framework for principal components analysis (PCA) on collections of networks via a specialized tensor decomposition we term Semi-Symmetric Tensor PCA or SS-TPCA. We derive computationally efficient algorithms for computing our proposed SS-TPCA decomposition and establish statistical efficiency of our approach under a standard low-rank signal plus noise model. Remarkably, we show that SS-TPCA achieves the same estimation accuracy as classical matrix PCA, with error proportional to the square root of the number of vertices in the network and not the number of edges as might be expected. Our framework inherits many of the strengths of classical PCA and is suitable for a wide range of unsupervised learning tasks, including identifying principal networks, isolating meaningful changepoints or outlying observations, and for characterizing the "variability network" of the most varying edges. Finally, we demonstrate the effectiveness of our proposal on simulated data and on an example from empirical legal studies. The techniques used to establish our main consistency results are surprisingly straightforward and may find use in a variety of other network analysis problems.