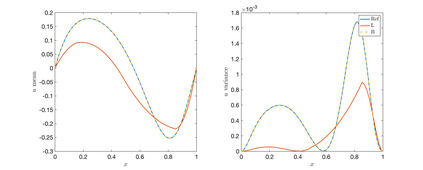
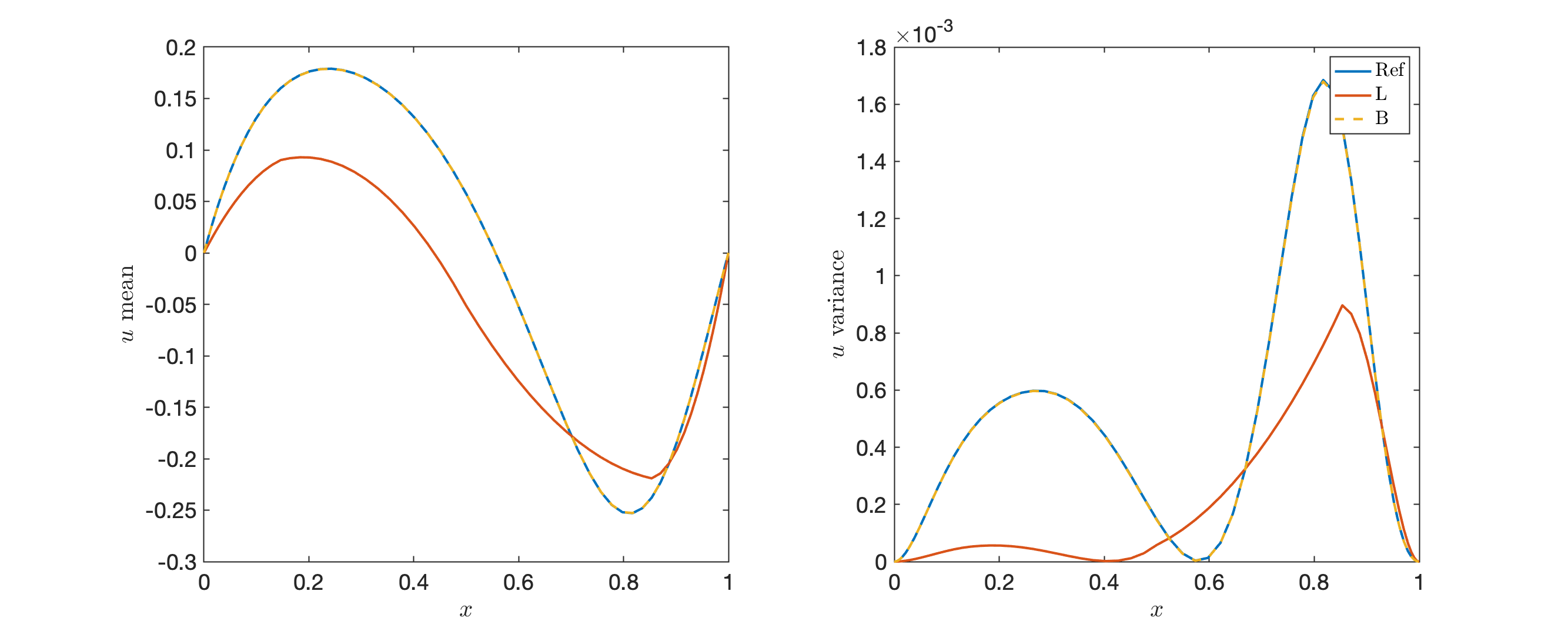
A ubiquitous challenge in design space exploration or uncertainty quantification of complex engineering problems is the minimization of computational cost. A useful tool to ease the burden of solving such systems is model reduction. This work considers a stochastic model reduction method (SMR), in the context of polynomial chaos (PC) expansions, where low-fidelity (LF) samples are leveraged to form a stochastic reduced basis. The reduced basis enables the construction of a bi-fidelity (BF) estimate of a quantity of interest from a small number of high-fidelity (HF) samples. A successful BF estimate approximates the quantity of interest with accuracy comparable to the HF model and computational expense close to the LF model. We develop new error bounds for the SMR approach and present a procedure to practically utilize these bounds in order to assess the appropriateness of a given pair of LF and HF models for BF estimation. The effectiveness of the SMR approach, and the utility of the error bound are presented in three numerical examples.
翻译:设计空间探索或复杂工程问题的不确定性量化方面的普遍挑战是尽量减少计算成本;减轻解决这类系统负担的一个有用工具是模型减少;这项工作考虑到在多盘混亂扩展的背景下采用随机模型减少方法,即利用低纤维样品形成一个随机减少的基础;由于基准的缩小,能够对少数高纤维样品的一定数量的利息进行双纤维性(BF)估计;成功的BF估计接近利息数量,其准确性与高频模型相似,计算费用接近于低频模型;我们为SMR方法制定了新的误差界限,并提出了实际利用这些界限的程序,以便评估特定一对LF和HFF模型对BF估计的合适性。 SMR方法的有效性和误差的效用在三个数字实例中作了介绍。