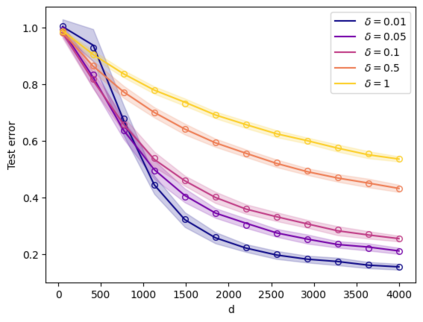
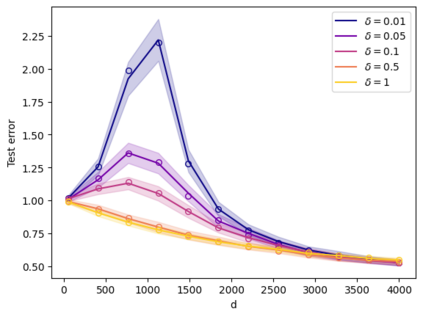
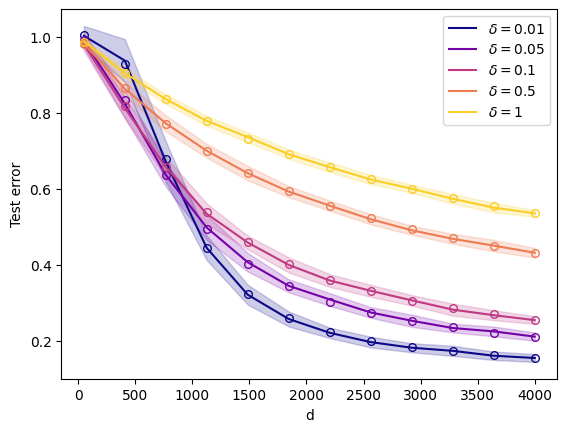
This paper develops some theory of the matrix Dyson equation (MDE) for correlated linearizations and uses it to solve a problem on asymptotic deterministic equivalent for the test error in random features regression. The theory developed for the correlated MDE includes existence-uniqueness, spectral support bounds, and stability properties of the MDE. This theory is new for constructing deterministic equivalents for pseudoresolvents of a class of correlated linear pencils. In the application, this theory is used to give a deterministic equivalent of the test error in random features ridge regression, in a proportional scaling regime, wherein we have conditioned on both training and test datasets.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2020年1月15日
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2024年2月5日
Arxiv
0+阅读 · 2024年2月1日
Arxiv
0+阅读 · 2024年2月1日