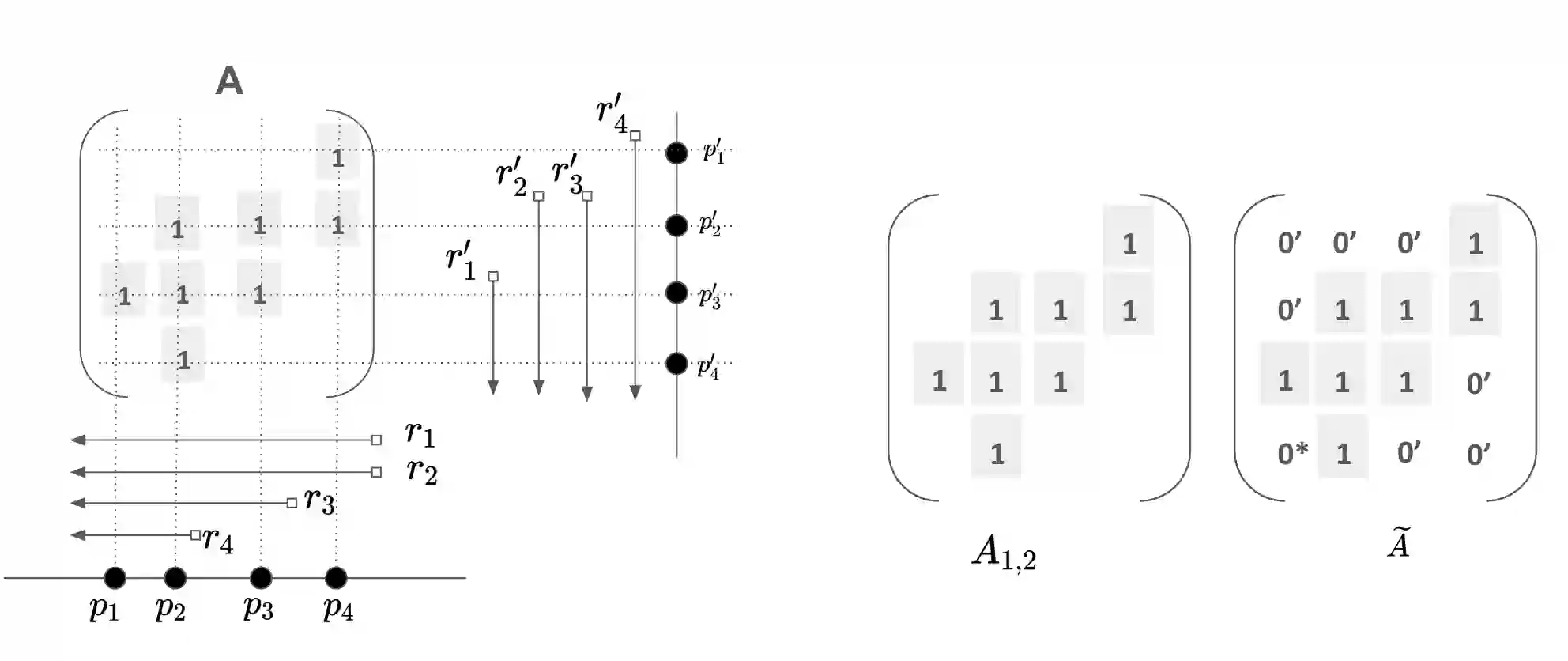
Ferrer dimension, along with the order dimension, is a standard dimensional concept for bipartite graphs. In this paper, we prove that a graph is of Ferrer dimension three (equivalent to the intersection bigraph of orthants and points in ${\mathbb R}^3$) if and only if it admits a biadjacency matrix representation that does not contain $\Gamma= \begin{bmatrix} * & 1 & * \\ 1 & 0 & 1 \\ 0 & 1 & * \end{bmatrix}$ and $\Delta = \begin{bmatrix} 1 & * & * \\ 0 & 1 & * \\ 1 & 0 & 1 \end{bmatrix}$, where $*$ denotes zero or one entry.
翻译：Ferrers维数与序维数同为二部图的标准维数概念。本文证明，一个图具有Ferrers维数三（等价于${\mathbb R}^3$中象限与点的交双图）当且仅当其存在一个双邻接矩阵表示，该表示不包含$\Gamma= \begin{bmatrix} * & 1 & * \\ 1 & 0 & 1 \\ 0 & 1 & * \end{bmatrix}$与$\Delta = \begin{bmatrix} 1 & * & * \\ 0 & 1 & * \\ 1 & 0 & 1 \end{bmatrix}$，其中$*$表示0或1元素。
相关内容
微信扫码咨询专知VIP会员