A primer on computational statistics for ordinal models with applications to survey data

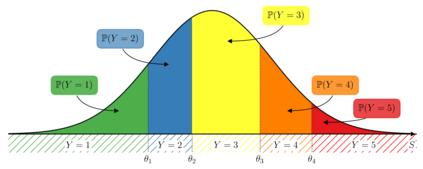
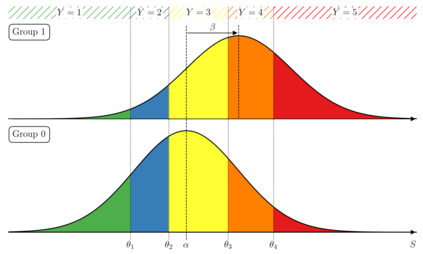
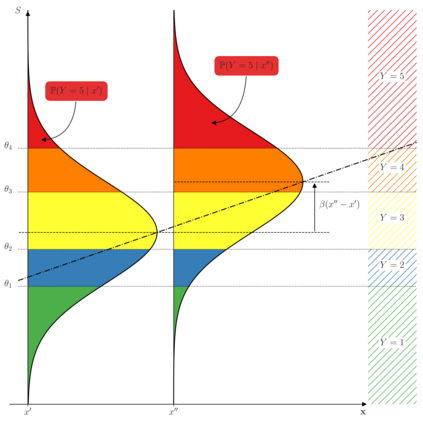
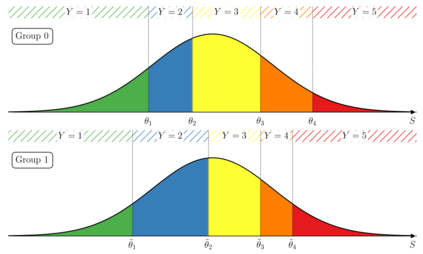
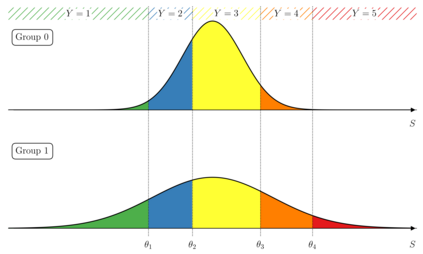
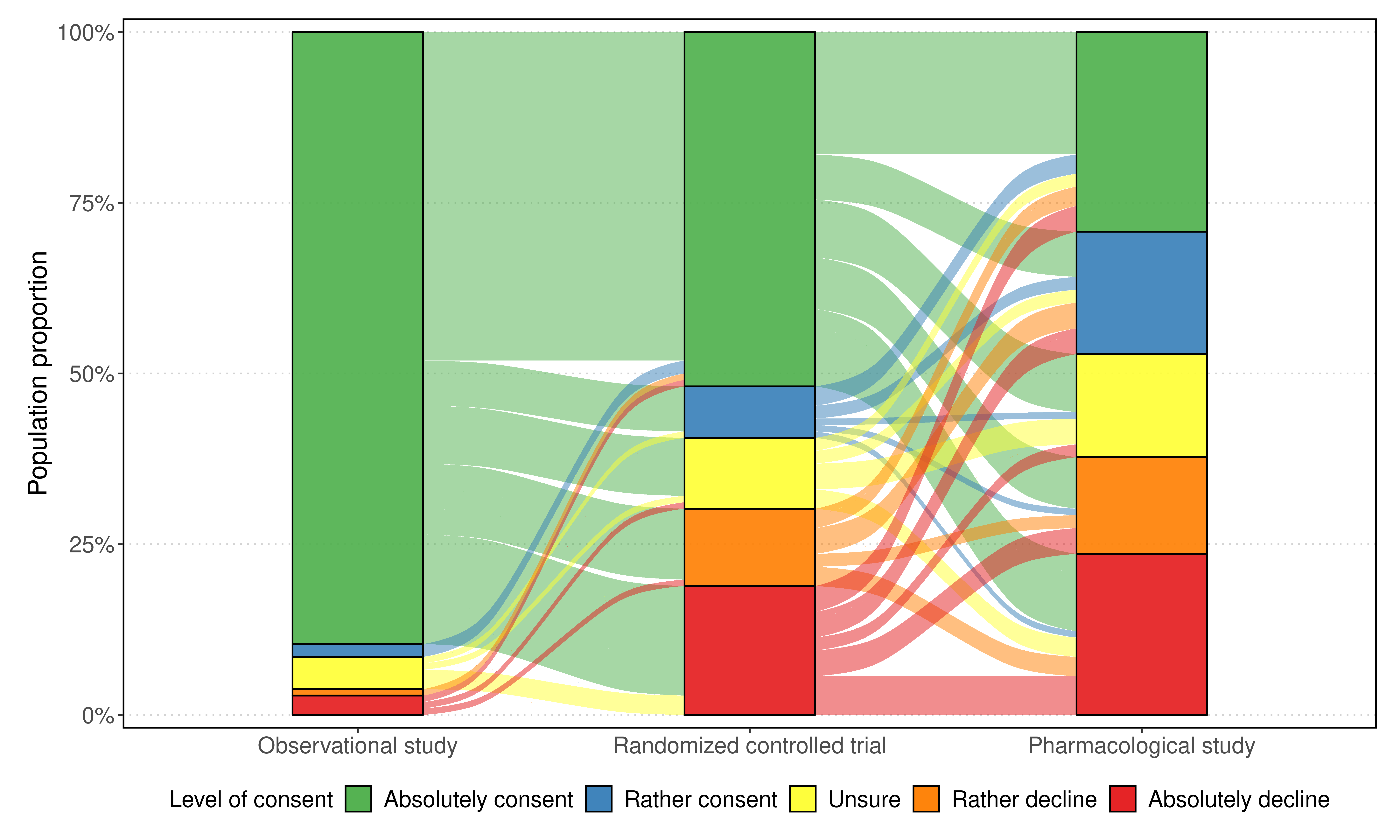
The analysis of survey data is a frequently arising issue in clinical trials, particularly when capturing quantities which are difficult to measure using, e.g., a technical device or a biochemical procedure. Typical examples are questionnaires about patient's well-being, pain, anxiety, quality of life or consent to an intervention. Data is captured on a discrete scale containing only a limited (usually three to ten) number of possible answers, of which the respondent has to pick the answer which fits best his personal opinion to the question. This data is generally located on an ordinal scale as answers can usually be arranged in an increasing order, e.g., "bad", "neutral", "good" for well-being or "none", "mild", "moderate", "severe" for pain. Since responses are often stored numerically for data processing purposes, analysis of survey data using ordinary linear regression (OLR) models seems to be natural. However, OLR assumptions are often not met as linear regression requires a constant variability of the response variable and can yield predictions out of the range of response categories. Moreover, in doing so, one only gains insights about the mean response which might, depending on the response distribution, not be very representative. In contrast, ordinal regression models are able to provide probability estimates for all response categories and thus yield information about the full response scale rather than just the mean. Although these methods are well described in the literature, they seem to be rarely applied to biomedical or survey data. In this paper, we give a concise overview about fundamentals of ordinal models, applications to a real data set, outline usage of state-of-the-art-software to do so and point out strengths, limitations and typical pitfalls. This article is a companion work to a current vignette-based structured interview study in paediatric anaesthesia.